|
|
|
|
|
|
 |
|
|
DIE KREISZAHL PI, DARGESTELLT ALS PI-FACHE QUADRATFLÄCHE IM N-ECK – EIN BEITRAG VON ANDREAS WEISS
|
|
 |
|
|
Seit der Onlinestellung dieser Internetseite
tetraktys.de im Dezember 2010 entstanden einige
sehr fruchtbare Kontakte zu querdenkenden
Menschen, welche die hier gesetzten Impulse
aufnahmen und weiter entwickelten.
Einer dieser kreativen Denker ist Andreas Weis,
der mich am 22.12.2013 auf einen interessanten
Zusammenhang zwischen der Kreiszahl Pi und
n-Ecken bzw. Simplexen aufmerksam machte.
Man stelle sich zuerst folgenden simplen
Sachverhalt vor:
An den vier Seitenflächen eines Quadrates befindet sich jeweils ein weiteres Quadrat
mit genau der gleichen Seitenlänge.
Klappt man nun diese insgesamt vier Quadrate
nach innen, überdecken sie sich restlos.
Es entstehen also vier komplette Überlappungen, die auf die rechten Winkel zurückzuführen sind.
Als nächstes fügen wir diesem Quadrat eine Ecke
hinzu, ein Fünfeck entsteht. Danach verfahren wir
in genau der selben Weise wie beim Viereck.
Zu beachten ist, dass die Kantenlänge stets
Länge Eins bleibt, weshalb sich mit zunehmender Eckenanzahl der Kreis auch vergrößert. An jeder Seite des Fünfecks
befindet sich wieder ein Quadrat entsprechender
Kantenlänge, also 1 Quadrat mehr = 5 Quadrate.
Nun klappen wir diese Quadrate wieder nach innen.
Da die Winkel sich ändern, ändern sich nun auch
die Schnittflächen.
Dabei konzentrieren wir uns nicht auf die
Flächendeckung des 5-Ecks, sondern schauen auf die Schnittfläche zweier geklappter Quadrate.
Multiplizieren wir eine Schnittfläche mit der Anzahl aller Schnittflächen (je Ecke) erhält man bereits den Wert 3,63.
Man kann also errechnen, dass die Gesamtflächendeckung, bzw. Gesamtschnittfläche der sich überlappenden Quadrate innerhalb eines dieser Quadrate im 5-Eck 3,63 Quadrate beträgt.
Führt man nun diese Geometrieübung mit
höheren n-Ecken weiter, so kommt man auf
folgende Werte:
4-Eck Gesamtschnittfläche =4
5-Eck Gesamtschnittfläche =3,63
14-Eck Gesamtschnittfläche =3,1954...
36-Eck Gesamtschnittfläche =3,1495...
160-Eck Gesamtschnittfläche =3,14196...
1187-Eck Gesamtschnittfläche =3,141599...
5467 Eck Gesamtschnittfläche =3,1415929...
Wie man unschwer erkennen kann:
Je mehr Ecken das n-Eck aufweist, um so
mehr nährt sich die Gesamtschnittfläche
dieses Einheits-Quadrats dem Wert Pi.
Mit jeder neuen Ecke kommt auch ein
Quadrat hinzu.
|
|
|
|
|
 |
|
Da auch das n-Eck, bzw. der Kreis größer wird
und damit auch die Gesamtschnittfläche der
Quadrate kleiner, verändert sich der Wert der Gesamtschnittfläche nur unwesentlich.
Diese Schnittmenge Pi (Fläche), die erst in der
Unendlichkeit stabil wird, entspricht genau den
Ursprungs-Flächeninhalt eines Kreises, nämlich
bei Radius = 1 ist der Flächeninhalt = Pi.
Weiterführend kann man nun die Aussage
machen, dass zur Berechnung des Flächen-
inhaltes eines Kreises A=Pi x r hoch 2
unser Pi nicht mehr zwingend nur ein
Faktor als Vervielfacher sein muss,
sondern Pi auch als Fläche dargestellt
werden kann, die mit dem Radius zum
Quadrat vervielfacht wird.
Stellt man Pi als Fläche dar, kann r nun als
Vervielfacher wirken und stellt in dieser
Betrachtungsweise selbst nur ein Vielfaches
des Einheitskreises (Basis) dar.
|
|
Ist also z.B. r gleich 5, bedeutet dies nur, dass
der Ursprung r=1 verfünfacht wird.
Dies wäre auch logischer, da das Flächenmaß
nicht erst entsteht durch Multiplikation, Meter
mal Meter, sondern die Fläche bereits besteht
in Quadratmeter, in Form von Pi und nur
vervielfacht wird.
Andreas Weiss
Wer diesen Sachverhalt vertiefen möchte,
der nehme bitte mit uns Kontakt auf unter:
info@tetraktys punkt de
(Das Wort "punkt" bitte mit . ersetzen.)
|
|
|
 |
|
Winkelsummen voller Kreise und Darstellung
als Sternpolygone in der Divisionstabelle
Alle aus den Überschneidungen der Quadrate
entstehenden Sternfiguren, so wie oberhalb
dargestellt, haben zwangsläufig die Innenwinkelsumme eines vollen Kreises.
Die entsprechenden Sternpolygone mit den
absolut deckungsgleichen Winkeln kann es
also nur in den geradzahligen Simplexen
bei folgenden Positionen innerhalb der
Divsionstabelle geben:
4/1 – Polygon
6/2 – Polygon mehrfach
8/3 – Sternpolygon
10/4 – Sternpolygon mehrfach !
12/5 – Sternpolygon
14/6 – Sternpolygon mehrfach
16/7 – Sternpolygon
18/8 – Sternpolygon mehrfach
20/9 – Sternpolygon
22/10 – Sternpolygon mehrfach
24/11 – Sternpolygon
26/12 – Sternpolygon mehrfach...usw. bis unendlich....
|
|
Was hier wieder auffällt, ist die Tatsache,
dass eben nur bis zu 10/4 alle vier Prinzipien
der Tetraktys enthalten sind!
Näheres unter:
DER SCHLÜSSEL ZUR TETRAKTYS
Alle nachfolgenden Positionen wiederholen
sich bis unendlich in 4-er Intervallen.
Weitere Auffälligkeiten in den oben
gezeigten Sternfiguren:
Bedingt durch die Tatsache, dass Mehrfach-
überlappungen der Quadrate mit zunehmender
Eckenzahl abnehmen müssem, ergibt sich:
5-Eck = 4-Fachüberlappungen.
6-Eck = 3-Fachüberlappungen.
7-Eck = 2-Fachüberlappungen.
Ab dem 7-Eck bricht außerdem im Zentrum
des Kreises ein "Loch" auf. Diese freie Fläche wächst selbstverständlich proportional zur Eckenanzahl und nähert sich bis unendlich der Pheripherie des Kreises.
Ab dem 12-Eck gibt es keine Mehrfach-
überlappungen mehr. Dieser Zustand einfacher Überlappungen gilt ebenfalls bis unendlich.
|
|
Man könnte nun schauen, ob die Zahlen 7 und 12 etwas gemeinsam haben, nun:
7 ist die Summe von 3 und 4
12 ist das Produkt von 3 und 4.
3- und 4-Eck sind jene zwei Möglichkeiten die
sich zwingend ergeben müssen, wenn man die
Mittelpunkte gleich großer Kreise verbindet,
welche so anordnet sind, dass sie einander
regelmäßig berühren. Eine dritte Möglichkeit,
das 6-Eck, entspricht dem selben
Packungsschema wie den 3-Ecken.
siehe:
KREIS, DREIECK & QUADRAT
Das gleiche gilt für Parkettierungen im Raum:
DIE GEOMETRIE DER LÜCKENLOSEN RAUMFÜLLUNG
Ganz sicher nicht unwichtig.
Wo nun die konkreten Schnittstellen sind und
was daraus herleitbar ist, müsste genauer
untersucht werden.
Achtung:
Die nun folgenden Zusammenhänge sind nur eine
Wiederholung aus dem Einführungstext!
|
|
 |
|
|
PYTHAGOREISCHE TETRAKTYS, PRIMZAHLEN UND DIE KREISZAHL PI
|
|
 |
|
|
Das Thema "Primzahlen" und "Sieb des Erathostenes" ist in der Divisionstabelle relativ einfach darstellbar. Genau genommen ist die Divisionstabelle geradezu prädestiniert, um die Primzahlverteilung visuell anschaulich zu machen – mit Hilfe von Punktemustern, ganz
im Sinne der Pythagoreer, hier zu sehen:
DAS SIEB DES ERATOSTHENES
& DIE TETRAKTYS
Etwas schwieriger zu zeigen ist das System hinter der unregelmäßigen Primzahlverteilung, aber es ist möglich! Mit Hilfe von 10-Punktedreiecken, was demnänchst unter diesem Link versucht wird.
Kommen wir nun zu noch anspruchsvolleren Sachverhalten, die auch Hauptgegenstand meiner Forschung sind, und deren Komplexität nicht nur schwer erfassbar, sondern leider auch schwer beschreibbar und darstellbar ist:
Es geht um die bis hier her bereits erläuterte Pythagoreische Tetraktys und deren Zusammenhang zwischen dem Primzahlproblem und der Kreiszahl Pi.
Dazu erachte ich es für sinnvoll, einige Fakten
kurz zu benennen, um die Dringlichkeit dieses
Zusammenhangs vor Augen zu führen:
Simplex Aufbau und Bedeutung:
Simplexe entsprechen in Wesen und Aussage der Kreiszahl Pi. So entspricht auch der Kreisumfang im Verhältnis zu seinem Durchmesser dem Verhältnis der natürlichen Zahl zu seinen möglichen Teilern!
Natürliche Zahl = n-Eck
Teiler = Tangenten durch den Kreis (n-Eck).
Weiter unten wird das deutlicher.
|
|
|
|
|
|
 |
|
Über die Hintergründe des offensichtlichen
Zusammenhangs zwischen Zahlentheorie
und der Kreiszahl Pi herrscht immer noch weitestgehend Unkenntnis!
Kreiszahl Pi und Riemannsche Vermutung:
Die Bedeutung von Pi in der Formel von
Leonard Euler ist bisher nicht bekannt:
|
|
|
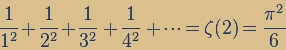 |
|
Simplex und Pascalsches Dreieck:
Weiter oben wurde beschrieben, wie sich die Weiterführung der Dimensionssprünge von Punkt, Linie, Fläche und Körper als geometrische Figuren an Stelle der Teilerpositionen in die Divisionstabelle integrieren lassen. Folgender Link macht das nachvollziehbar:
SIMPLEX – DER FESTE AGGREGATZUSTAND DER ZAHL
Es gibt aber noch eine andere direkte Verbindung zur Zahlentheorie – das Pascalsche Dreieck!
Einzelheiten unter:
SIMPLEX – MULTIDIMENSIONALE TETRAEDER, 4.DIMENSION
Also auch mit diesem Sachverhalt ist eine Brücke geschlagen zwischen der Zahlentheorie und den Simplexen = Kreisgeomerie = Kreiszahl Pi.
Aber der wichtigste Lösungsansatz ist meiner Meinung nach in der Tatsache zu finden,
dass es starke Korrelationen zwischen den
Innenwinkelsummen der Simplexe und den
entsprechenden Teilerpositionen innerhalb
der Divisionstabelle gibt.
Dazu folgendes:
|
|
Ein interessanter Hinweis aus Wikipedia:
Die relative Häufigkeit, dass zwei zufällig
gewählte natürliche Zahlen, die unterhalb
einer Schranke M liegen, teilerfremd sind,
strebt mit:
|
|
|
 |
|
|
|
Dies entspricht dem Verhältnis zwischen der Menge der rot markierten Felder zu den restlichen Feldern in der Divisionstabelle.
Ein Zusammenhang zwischen der Ziffer 25
und der Kreiszahl Pi:
Weiter oben wurde im Zusammenhang mit der arithmetischen Entsprechung des Pentagramms (2,5) auf die erste Pseudoprimzahl, nämlich die 25 hingewiesen.
Das Verhältnis Kreisfläche zu Quadrat
entspricht 78,5%.
Pi x 25 = Kreisfläche zu Quadratfläche,
also: Pi x 25 = 78,53981633...
Zu Quadrat- und Kreisfläche siehe darunter.
|
|
|
 |
|
|
|
|
|
 |
|
Wo steckt in der Tetraktys = Vierheit der Kreis?
Eine erste Antwort dazu ist so simpel, dass
sie es scheinbar nicht wert ist, von der
Menschheit beachtet zu werden:
Das Viereck ist das einzige Polygon,
dessen Innenwinkelsumme genau
einen Vollreis ergibt!
Es wird immer betont, dass das Dreieck eine
Winkelsumme von 180 Grad hat ( 3 x 60 Grad ).
Aber kaum jemand misst der Tatsache eine
Bedeutung bei, dass das Viereck (Quadrat) eine
Winkelsumme von 360 Grad aufweist,
( 4 x 90 Grad ), denn dies entspricht bekanntlich einem vollen Kreis.
Das Fünfeck hat eine Winkelsumme von
540 Grad, dies entspricht 1,5 Vollkreisen. Die Primzahl 5 durchbricht also eine bestehende
in sich abgeschlossene Ordnung!
Siehe Animation:
|
Die von Menschen erdachte Grad-Einteilung ist
allerdings in diesem Fall völlig unwichtig.
Hier geht es um die Vielfachen eines vollen
Kreises!
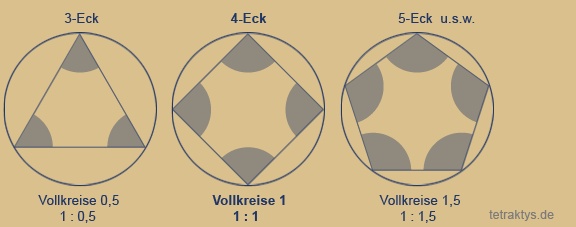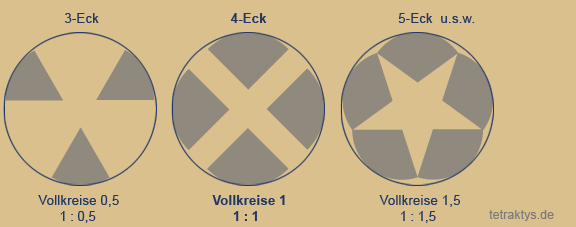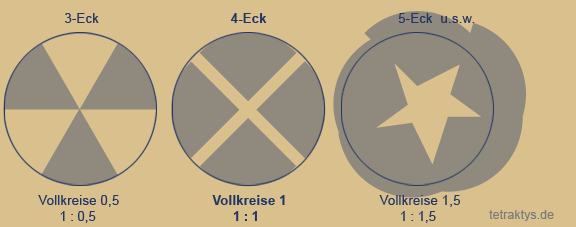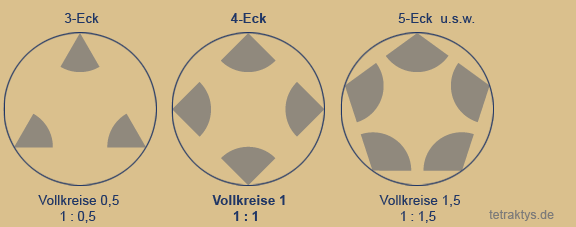
Zur Animation rechts :
Die Peripherie des Kreises bilden die natürlichen
Zahlen, dargestellt als eingezeichnete Polygone,
also n-Ecke! ( n = natürliche Zahl )
Die Ziffer 1 stellt den Mittelpunkt des
Kreises dar. Der Durchmesser des Kreises stellt
die Ziffer 2 dar. Das Dreieck ist das erste "echte"
Polygon, welches sich in einem Kreis
einzeichnen lässt.
Das Viereck nun ist das erste Polygon, in dem
sich Tangenten einzeichnen lassen, die direkt
durch den Mittelpunkt laufen.
Mit dem Fünfeck können wir zum ersten Mal ein
Sternpolygon einzeichnen. Dabei bilden die
Tangenten Überschneidungen. Das Ergebnis ist
ein Pentagramm.
|
|
|
 |
|
|
Führt man dieses System weiter, so entstehen
um so mehr Überschneidungen der Tangenten,
je größer die entsprechende Zahl ist.
Es entstehen Simplexe.
Simplexe sind zweidimensionale Projektionen
multidimensionaler Tetraeder, (Tetra(!)eder.
Diese Zusammenhänge gehen noch viel
weiter und gipfeln tatsächlich wieder in diesen
1 + 2 + 3 + 4 = 10 !
Zu diesem Tatbestand hier eine detailierte
Zeichung: tetraktys 1.pdf
oder etwas ausführlicher:
SIMPLEX – DREIECKSZAHLEN &
DEZIMALCODIERUNG
|
|
|
 |
|
|
Die Peripherie des Kreises bilden die
natürlichen Zahlen, dargestellt als
eingezeichnete Polygone, also n-Ecke
( n = natürliche Zahl ).
Die eben beschriebenen Überschneidungen
innerhalb des Kreises von der Peripherie bis
zum Mittelpunkt ergeben die Reihe
natürlicher Zahlen, mit denen die Zahlen
der Peripherie geteilt werden.
Die dadurch entstehenden vielfachen
Überschneidungen bilden ein Gitternetz
aus kleinen Vierecken.
Diese Vierecke stellen ein Koordinatensystem
innerhalb der Geometrie des Kreises dar.
Sehen Sie dazu die Animation rechts:
Die geometrische Veranschaulichung der
Teilbarkeit natürlicher Zahlen am Beispiel vom
Simplex des 30-Eck.
Somit ergibt sich das kartesische
Koordinatensystem im Kreis, das mit dem
Lambdoma gleichgesetzt werden kann,
welches in der Musiktheorie bzw. der
Harmonik bekannt ist.
Umgekehrt kann man aber auch die
einzelnen Sternpolygone der Simplexe
in das Lambdoma auffächern.
Zusammenfassung:
Der Kreis beschreibt zwei Zahlengeraden:
die erste Zahlenreihe bildet den Kreisumfang
selbst, die zweite Zahlenreihe, als Teiler der
ersten Zahlengerade, bildet den Radius, bzw.
den Durchmesser des Kreises.
|
|
|
Durch die Doppelung gerader und ungerader
Zahlen innerhalb dieses kartesischen
Koordinatensystems in der Geometrie des
Kreises manifestiert sich die Pythagoreische
Tetraktys!
|
|
|
|
Die Geometrie der Simplexe (eigentlich multidimensional!) ist nur >eine< wenn auch
eine allumfassende Möglichkeit, um die
Pythagoreische Tetraktys zu veranschaulichen.
Denn auch in unserem 3-dimensional, erfahrbaren
Raum lässt sich die Pythagoreische Tetraktys
erkennen.
Was immer man sich genau darunter vorstellen
muss, dass soll nun hier auf dieser Internetseite
im einzelnen erörtert werden.
Es steht ohnehin außer Frage: Die Geometrie des Kreises ist mit der Teilbarkeit natürlicher Zahlen verknüpft.
Neue Erkenntnisse bei der Forschung zur
Riemanschen Vermutung bestätigen die
Schlüsselrolle der Kreiszahl Pi für das
Verständniss in tiefere Zusammenhänge
der Primzahlverteilung.
Man ist sich heute auch darüber einig, dass
tiefere Erkenntnisse zur Problematik der
Riemanschen Zetafunktion zu neuen
bahnbrechenden Erkenntnissen in der
Physik führen werden.
Bei weiteren Betrachtungen werden wir sehen,
dass hinter diesem harmlos daherkommenden:
1 + 2 + 3 + 4 = 10 sehr viel mehr steckt, als
etwas Esoterik, vage Vermutungen oder antike
Philosophie. Denn das, was sich hinter dem
abstrakten Begriff "Tetraktys" verbirgt, beantwortet
eines der größten ungelösten Probleme der
Zahlentheorie: die (Un)-Ordnung in der
Primzahlverteilung.
Und ganz wichtig:
Das alles > ohne < Dezimalsystem.
Denn dieses darf kein Aufhänger für die Ziffer
Zehn der Pythagoreischen Tetraktys sein.
|
|
 |
|
|
Mit diesem kurzen Überblick soll erst mal nur ein
erster Eindruck entstehen, wie diese spezielle
Geometrie und die Zahlentheorie miteinander in
Beziehung stehen.
Das wirklich Wertvolle an dieser Geometrie
aber ist die Tatsache, dass wir mit ihr in der
Lage sind, uns von den Denkbarrieren des
Dezimalsystems frei zu machen.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|