|
|
|
Dieser folgende, visuell sehr ansprechende Sachverhalt eröffnete mir damals im Jahre 2006 das Tor zur Pythagoreischen Tetraktys
Damals kam mir eine Idee, die nicht ganz
einfach zu beschreiben ist. Zwar werde
ich es weiter unten versuchen, aber der Leser
sei beruhigt, man muss es nicht sofort
verstehen, entscheidend ist erst mal nur,
das Ganze auf sich wirken zu lassen.
An jenem Tag zeichnete ich wieder diese
Gebilde welche man "Simplex" nennt, in
einem vektorbasierten Zeichenprogramm.
Dazu zeichnet man ein Vieleck (Polygon)
und zeichnet in dieses Vieleck so genannte Sternpolygone.
Dann kam mir ein folgenschwerer Einfall und mit einem einzigen Mausklick erschienen vor meinen Augen plötzlich wunderschöne Ornamente! |
|
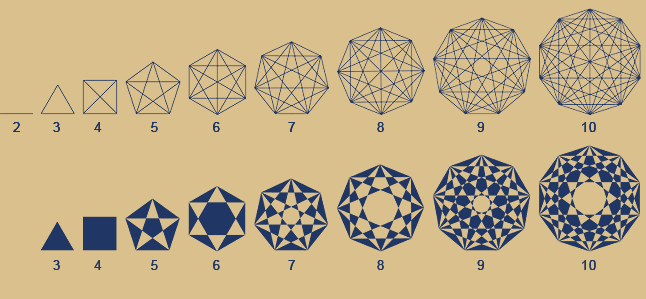
Das Ergebnis sieht nicht nur nett aus, sondern birgt eine Überraschung!
Aber vielleicht entdecken Sie bei aufmerksamer Betrachtung die Tetraktys (= Vierheit) in der Abfolge dieser Ornamente ja schon selbst!
|
|
Und halten sie sich folgende Tatsache vor Augen: Jedes Ornament präsentiert den genauen Charakter der jeweiligen darunter stehenden Zahl, dh. die Teilbarkeit durch natürliche Zahlen. Erläuterungen ganz unten. |
|
|
|
 |
|
|
 |
|
|
|
Was also tat ich und was führte der Rechner zu Ende?
In jedes Polygon habe ich die maximal mögliche Anzahl von Sternpolygonen gezeichnet. Dabei bin ich in der Weise verfahren, wie ganz unten auf dieser Seite zu sehen ist.
Dann kam mir folgender Einfall: Ich füllte per Mausklick die Fläche des Polygons und die Flächen seiner eingezeichneten Sternpolygone mit einer Farbe und führte im Vektor-Zeichenprogramm den Befehl aus "Objekte verbinden".
Auf diese Weise entstehen "alternierende Füllungen".
Das bedeutet, dass alle Flächen, die durch die Überschneidungen entstehen, abwechselnd mit Farbe gefüllt oder nicht gefüllt werden.
Da aber nun bei den Simplex, welche die geraden Zahlen präsentieren, die letzten Tangenten direkt durch den Mittelpunkt laufen und als Linien eben keine Fläche bilden, fallen diese Tangenten einfach raus!
|
|
Das ist auch der Grund, weshalb geradzahlige Ornamente ein größeres "Loch" in der Mitte aufweisen als die ungeradzahligen.
Damit haben wir nun zwar die Frage nach dem "Wie" beantwortet (was habe ich gezeichnent und was hat der Computer daraus gemacht), aber das "Warum" ist damit noch nicht geklärt!
Warum entsteht dieser Wechsel nach jeweils >4< Ornamenten?
Diese Frage habe ich mindestens 4 Mathematikern gestellt, aber leider konnte mir kein einziger Zahlenjongleur eine plausible Antwort darauf geben! Also musste ich mich selbst an die Lösung dieses Problems machen.
Um also der Sache auf den Grund zu gehen, fächerte ich die in die Polygone einzeln eingezeichneten Sternpolygone in einem Koordinatensystem auf, so wie es hier darunterstehend zu sehen ist:
|
|
|
|
Wo also steckt in diesen Ornamenten allein schon für den rein visuellen Betrachter die Tetraktys?
Am auffälligsten sind diese ersten vier mit Farbe gefüllten Simplex welche die Zahlen 3 bis 6 vertreten. Das Zentrum ist mit Farbe gefüllt, die nächsten vier Simplex der Ziffern 7 bis 10 haben einen "leeren" Mittelpunkt.
Ab der Ziffer 11 haben die nächsten vier Figuren wieder einen gefüllten Mittelpunkt.
In diesem Wechsel geht es immer weiter
bis in alle Ewigkeit – wie ich später erkannte.
Wie entsteht dieser "Vierertakt"?
Was habe ich gezeichnet und was hat der Computer (das Vektor-Zeichenprogramm) daraus gemacht?
Nun brauchte man ja einem "Vierertakt" keine größere Bedeutung beimessen, der aus einer
Laune eines Grafikers und der Willkür des
Computers entsteht! Aber hier wollte es der Zufall, dass Mensch und Maschine auf die Pythagoreische Tetraktys stießen.
|
|
|
|
 |
|
|
 |
|
|
Oben in der Waagerechten befindet sich der Zahlenstrahl von 1 bis unendlich mit den geometrischen Entsprechungen der Simplex bzw. Ornamente, rechts in der Senkrechten sehen Sie die Anzahl der aufkumulierten Stufen. Was eigentlich ist mit dem Begriff "Stufe" gemeint? Schauen wir uns die aufgefächerten Sternpolygone genauer an.
Die erste waagerechte Reihe unter den Ornamenten sind die Polygone selbst, die einfach nur mit Farbe gefüllt sind. Die zweite Reihe präsentieren alle Sternpolygone, bei denen jeder zweite Eckpunkt verbunden ist. Deshalb muss die Peripherie auch zweimal komplett abgegriffen werden um alle Eckpunkte zu erreichen.
Es sind also zwei Umläufe nötig, infolgedessen es zu einer Überschneidung kommt! Das Ergebnis sind zwei Stufen: die äußere Stufe (Sternzacken) ist mit Farbe gefüllt, wärend die innere Stufe leer ist.
Mit diesem Prinzip geht es immer weiter. Jedes nachfolgende Sternpolygon hat ein Stufe mehr als der Vorgänger, da immer ein Eckpunkt mehr ausgelassen wird! Infolgedessen hat jedes nachfolgende Sternpolygon spitzwinkligere Zacken als der Vorgänger.
Gerade Zahlen schließen immer mit einem
"Linienstern" ab. Dieser fällt aus dem System raus, da er keine Fläche aufweist.
Wo also entstehen diese Wechsel von gefülltem
zu nicht gefülltem Mittelpunkt und umgekehrt?
Beim Betrachten der Zahlenfolgen entdeckte ich
schließlich die Lösung:
Genau da, wo der waagerechte als auch der senkrechte Zahlenstrahl eine ungerade Zahl enthalten, da kommt es zu einem Wechsel!
Auch in einem Koordinatensystem "doppelt" sich dieser Effekt, und es kommt zu einem "Vierertakt"!
Die Ursache dieser Doppelung wiederum ist, dass Tangenten durch ein Polygon –
ausgehend von einem Eckpunkt der
Peripherie – naturgemäß eben nur bis
zum Mittelpunkt laufen.
Ist der Mittelpunkt ("Nullpunkt") überschritten,
wiederholt sich das Schema und die selben Sternfiguren überlagern sich einfach nur.
Daraus ergibt sich auch die Tatsache, dass ein entsprechendes Koordinatensystem nur zu genau einem vierten Teil mit den relevanten Sternpolygonen gefüllt sein kann, Die Tabelle rechts zeigt es.
Und genau dieser Sachverhalt wird in anderen Themenbereichen auf dieser Internetseite auch eingehender untersucht.
Letztendlich beinhalten alle Sternpolygone von geradzahligen Simplexen Winkelsummen von immer jeweils vollen Kreisen, wogegen alle Sternpolygone ungeradzahliger Simplexe Winkelsummen mit Kommawerten enthalten, da zusätzlich immer ein halber Vollkreis hinzukommt.
Unter den folgenden Link versuche ich ausführlicher diese geometrischen Eigenschaften der Simplexe darzustellen:
SIMPLEX – DREIECKSZAHLEN & DEZIMALCODIERUNG
hier eine Kurzfassung als PDF-Datei: tetraktys_1.pdf
Nun muss aber der Leser nicht glauben,
dass allein diese Vierheit bei mir schon
ein "Tetraktys-Erlebnis" hervorrief!
Denn schließlich heisst es doch:
1 + 2 + 3 + 4 = 10 !
Was also ist mit der Ziffer 10?
Die aufkumulierten Stufen ("Stufen gesamt"), welche unterhalb der Klammern zu sehen sind, zeigen die Abfolge der Dreieckszahlen.
Das 10-Eck ist der einzige Simplex, bei
welchem die Anzahl der Ecken
mit der Anzahl der Stufen übereinstimmt,
kleinere Simplex haben weniger "Stufen"
als Ecken, größere Simplex haben mehr
Stufen als Ecken!
Man müsste dieser Tatsache keinerlei Bedeutung beimessen, wenn:
1. einige andere Symmetrien nicht das
Gleiche zeigen würden, siehe
DAS PUNKTEDREIECK,
EINFACH NUR 1 + 2 + 3 + 4 = 10 ?
2. ganz offensichtlich ein zahlentheoretischer Zusammenhang, nämlich in Bezug auf die Primzahlverteilung besteht
3. das Pascalsche Dreieck die Bedeutung dieser Zusammenhänge stützt.
|
|
|
 |
|
Es geht dabei um die Übereinstimmung
der Stufen!
Die dunklen Felder des Pascalschen Dreiecks enthalten bekanntlich nur ungerade Zahlen, die hellen Felder nur gerade Zahlen.
Schauen Sie sich die Animation der oberen Tabelle länger an, und achten Sie auf folgendes:
Oben in der Tabelle:
der Zahlenstrahl entsprechend den n-Ecken
Vertikal ganz rechts in der Tabelle:
Die Anzahl der Stufen pro Umlauf = Teiler von n, entspricht der n-Folge im Pascalschen Dreieck (1,2,3,4,5,6…).
Unterhalb der Tabelle:
Die Anzahl der Stufen gesamt = Dreieckszahlen, entspricht den Dreieckszahlen im Pascalschen Dreieck (1,3,6,10,15,21…).
Beispiel:
Die ungeraden Dreieckszahlen im Pascalschen Dreieck 1 und 3 beinhalten die vier Ziffern 3,4,5,6
Die geraden Dreieckszahlen im Pascalschen Dreieck 6 und 10 beinhalten die nächtsten vier Ziffern 7,8,9,10 usw….also gemäß dem Vierertakt der Ornamente
|
|
Dieser hier gezeigte Sachverhalt ist außerdem ein
äußerst prägnantes Beispiel für pythagoreische
Zahlenmystik, die heutzutage auf Unverständnis
trifft, weshalb sie ja auch als "mystisch"
abgehakt wird:
Die Pythagoreer haben die ungeraden Zahlen als
männlich aktives Prinzip gesehen, wogegen sie
den geraden Zahlen einen weiblich passiven
Charakter zugesprochen haben.
Wir treffen also bei diesem hier gezeigten Beispiel gleich auf drei typisch pythagoreische Themenkreise:
1. die Tetraktys selbst,
2. Charakter gerader und ungerader Zahlen
3. das Pentagramm, das Erkennungszeichen
der Pythagoreer.
Denn jenes vierte Sternpolygon des 10-Ecks setzt sich aus zwei Pentagrammen zusammen.
Speziell in der hier behandelten Primzahlthematik geht es genau um diese zwei Pentagramme, siehe als Einstieg:
DER SCHLÜSSEL ZUR TETRAKTYS
|
|
|
|
 |
|
|
Zum besseren Verständnis hier noch einmal kurz die zahlentheoretische Entsprechung der Geometrie der Simplex am Beispiel des 10-Eck-Simplex:
|
|
|
|
 |
|
|
Das 10-Eck,
jeder Eckpunkt wird verbunden.
|
|
Verbinden wir jeden 2. Eckpunkt, so müssen wir auch zweimal um das Zentrum des 10-Ecks fahren. Dabei entstehen zwei Fünfecke (Pentagone).
|
|
Verbinden wir nun jeden 3. Eckpunkt, dann müssen wir dazu den Mittelpunkt auch dreimal umrunden. Dabei entsteht ein Sternpolygon, welches wir in einem Zug zeichnen können.
|
|
Verbinden wir nun jeden 4. Eckpunkt, dann müssen wir dazu den Mittelpunkt auch viermal umrunden. Dadurch entsteht die letzte, in einem 10-Eck mögliche Sternpolygon-Konstellation, sie setzt sich aus zwei Pentagrammen (Fünfsternen) zusammen.
|
|
Verbinden wir nun jeden 5. Eckpunkt, dann können wir von Eckpunkt zu Eckpunkt nur noch Linien zeichnen, welche direkt durch den Mittelpunkt ("Nullpunkt") laufen. Diese Liniensterne haben in mehrfacher Hinsicht einen
"Null-Status", siehe auch:
tetraktys_1.pdf |
|
Hier sehen wir noch einmal den vollständigen
Simplex.
|
|
|
 |
|
|
10 geteilt durch 1
bzw. 1 x 10
|
|
10 geteilt durch 2
bzw. 2 x 5
|
|
10 geteilt durch 3
bzw. 3 x 3,333...
|
|
10 geteilt durch 4
bzw. 4 x 2,5
|
|
10 geteilt durch 5
bzw. 5 x 2, entspricht
der zweiten Konstellation = 2 x 5
|
|
|
|
^ Zurück nach oben zum Menü ^
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|