|
|
|
|
|
|
|
|
|
|
|
 |
|
Zu diesem Thema Wikipedia 10.01.2012:
In der Geometrie ist die n-te Kusszahl
(auch Kontaktzahl) die maximale Anzahl
an n-dimensionalen Einheitskugeln, also
Kugeln mit Radius 1, die gleichzeitig eine
weitere solche Einheitskugel im euklidischen
Raum berühren können, ohne dass
Überschneidungen auftreten.
Zusätzlich kann die Bedingung aufgestellt
werden, dass die Mittelpunkte der Kugeln
in einem Gitter liegen müssen
(Gitterkusszahlen).
Als Kusszahlenproblem ist das Fehlen einer allgemeinen Formel zur Berechnung der Kusszahlen bekannt.
Hier von mir eine wissenschaftlich nicht korrekte, aber vielleicht allgemeinverständlichere Erklärung:
Kusszahl = Die maximal mögliche Anzahl
von gleich großen "Umkugeln", die eine
"Zentralkugel" berühren können.
Für jede Dimension gibt es eine
eigene Kusszahl.
In der ersten Dimension (Linie) ist die Einheitskugel eine Strecke, an deren Endpunkten jeweils eine weitere Strecke hinzugefügt werden kann.
|
|
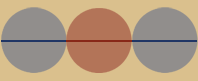
Die Kusszahl für Dimension 2 ist folglich 6.
Der Zentralkreis in der Mitte ist rotbraun dargestellt, die 6 Umkreise graublau.
In der dritten Dimension (Raum) haben wir auch dreidimensionale Körper, aus Kreisen werden demnach Kugeln. |
|
12 gleich große Kugeln passen genau um
eine 13. Kugel, siehe die zwei Abbildungen oben rechs. Beide Bilder zeigen die selbe Struktur, es handelt sich lediglich um zwei verschiedene Symmetrieansichten.
Die Kusszahl für Dimension 3 ist folglich 12.
|
|
|
 |
 |
|
|
|
 |
|
|
 |
|
|
Kubooktaeder |
|
Die Kusszahl für Dimension 1 ist folglich 2.
In der zweiten Dimension (Fläche) ist die
Einheitskugel ein Kreis. 6 gleichgroße Kreise
passen genau um einen 7. Kreis!
siehe die Abbildung oben links.
|
|
|
|
Dies entspricht einem Ausschnitt der Kepplerschen
Kugelpackung, es handelt sich dabei wieder um
das so genannte kubisch flächenzentrierte Gitter.
Verbindet man die Mittelpunkte der Kugeln, dann ergeben die Außenkonturen ein Kubooktaeder.
|
|
Das Kubooktaeder setzt sich aus 4 ineinander verschränkten 6-Ecken zusammen. 4 x 6 = 24.
Siehe Abbildung in der Mitte.
Oder anders betrachtet:
Das Kubooktaeder hat 24 Kanten.
|
|
 |
|
Wie sieht es nun mit den theoretisch möglichen Dimensionen oberhalb unserer 3. Dimension aus?
Dazu Wikipedia weiter:
Erst Anfang des 21. Jahrhunderts wurde
bewiesen, dass die Kusszahl für die vierte
Dimension die Zahl 24 ist.
Florian Pfender, Günter M. Ziegler
Ferner sind die Kusszahlen für die Dimensionen
n = 8 (240) und n = 24 (196.560) bekannt;
im 24-dimensionalen Raum werden die Kugeln
auf den Punkten des Leech-Gitters platziert,
sodass kein Platz übrig ist.
|
|
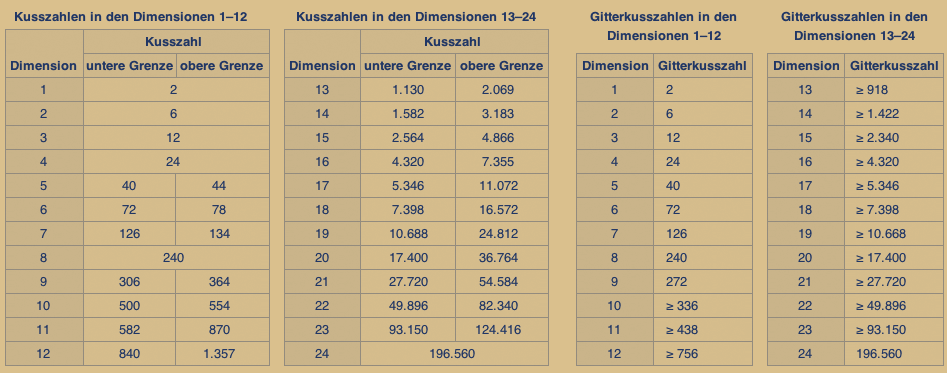
Die folgende Tabelle gibt die bekannten Grenzen
für die Kusszahl bis zur Dimension 24 wieder.
Wikipedia Ende.
Unten sehen Sie die entsprechenden Tabellen,
die auch in Wikipedia zu finden sind.
Zu sehen sind die absoluten Werte, die im Zusammenhang mit der Ziffer 24 errechnet wurden, wärend alle anderen Werte Von-Bis-Werte sind.
In diesem Zusammenhang ist also das
Leech-Gitter interessant. |
|
Unabhängig von der Tatsache, dass mit dem Beweis der Kusszahl 24 der vierten Dimension vermutlich auch die entsprechenden Vielfachen von 24 korrekt ermittelt werden konnten.
Denn:
Fakt ist die Tatsache, dass die Ziffer 24 in den
Fraktalen von Kugelpackungen innerhalb
des dreidimensionalen Raumes aus
kombinatorischen Gründen eine wichtige
Rolle spielen muss.
|
|
 |
|
 |
|
|
 |
|
|
Obige Anmerkung von der Bedeutung dier Ziffer 24 in den Fraktalen von Kugelpackungen innerhalb des dreidimensionalen Raumes möchte ich im folgenden kurz erläutern:
Die Flächen der Kristallgitter von Kugelpackungen setzen sich ausschließlich
aus Dreiecken, Quadraten bzw. auch
Sechsecken ( 6 Dreiecke ) zusammen.
Das wiederum hängt mit der Tatsache zusammen, dass eben nur genau diese drei Polygone in der Ebene mit sich selbst allein oder im Raum miteinander kombiniert, lückenlos pflasterbar sind.
Hier zuerst mal die wichtigsten Symmetrien, die in den Kristallgittern von Kugelpackungen vorkommen:
Hexaeder: 6 x 4-Ecke = 24
Oktaeder: 8 x 3-Ecke = 24
Sterntetraeder: 24 x 3-Ecke
Kubooktaeder: 3 x 8, oder 4 x 6 = 24
Tetraeder: 4 x 3-Ecke = 24 / 2
Nun muss man sich vor Augen halten, dass es sich bei Kristallgittern von Kugelpackungen tatsächlich um echte Fraktale handelt!
Genau genommen handelt es sich unter anderem auch um dreidimensionale Sierpinski-Dreiecke, also Sierpinski-Tetraeder und
-Oktaeder!
Da nun die Anzahl der Fraktale der jeweiligen Iterationsstufe eines n-Ecks identisch mit seinen Ecken ist, haben diese Symmetrien in der ersten Iterationsstufe ebenfalls immer entsprechende "fraktale Flächen".
|
|
Konsequenterweise sieht das so aus:
Oktaeder: 3 x 8 = 24 Flächen gesamt
Hexaeder: 4 x 6 = 24 Flächen gesamt
Sterntetraeder: 3 x 24 Flächen gesamt
Kubooktaeder: 3 x 8, oder 4 x 6 = 24
Flächen gesamt
Tetraeder: 3 x 4 = 12 Flächen gesamt
|
|
|
Der dreidimensionale Raum lässt sich nur mit drei der fünf platonischen Körper lückenlos füllen: mit Oktaeder und Tetraeder im Verbund, oder mit Hexaedern (Würfeln) allein.
Sterntetraeder und Kubooktaeder sind lediglich aus diesen drei Körpern zusammengesetzt.
Wenn also diese "Geometrie der lückenlosen
Raumfüllung" in mehrfacher Weise mit der
Ziffer 24 korreliert, könnte es dann sein,
dass diese hoch zusammengesetzte Zahl
nicht nur bei der Primzahlverteilung eine
wichtige Rolle spielt, sondern auch
unmittelbar mit dem Raum selbst tun hat?
Interessanterweise spielt die Zahl 24 im Zusammenhang mit einem 4-dimensionalen Raum auch in Peter Plichtas Überlegungen
die tragende Rolle.
Was aber noch viel bemerkenswerter ist:
Kusszahlen und Kristallgitter von Kugelpackungen werden von Plichta überhaupt nicht erwähnt, andererseits spielt das Sierpinskidreieck in seinen Ausarbeitungen eine wichtige Rolle!
Plichtas Theorien gibt es schon weit über 20 Jahre. Aber erst 2006 wurde die Kusszahl 24 in der theoretisch 4. Dimension mathematisch bewiesen! In wieweit also auch hier ein
direkter Zusammenhang besteht, sollte
untersucht werden.
Siehe dazu auch:
DIE GEOMETRIE DER LÜCKENLOSEN RAUMFÜLLUNG |
|
|
 |
|
Die Abbildung zeigt ein Fraktal des Oktaeders
in der ersten Iterationsstufe. Jede Dreiecksfläche teilt sich – genau wie beim Sierpinski-Dreieck – in drei kleine Dreiecke auf. Dabei entstehen 24 Oktaederflächen. Schneidet man die Spitzen weg, haben wir wieder ein Kubooktaeder.
|
|
 |
|
 |
|
|
PYTHAGOREISCHE TETRAKTYS UND CHRISTLICHE RELIGIONSPHILOSOPHIE ZUM THEMA KUSSZAHLEN
|
|
 |
|
|
|
Die Pythagoreische Tetraktys
und die christliche Religionsphilosophie
zum Thema "Kusszahlen":
Dazu noch einmal die Kusszahlen in den einzelnen Dimensionen:
Dimension 1: 2 Linien um eine 3.
Dimension 2: 6 Kreise um einen 7.
Dimension 3: 12 Kugeln um eine 13.
Dimension 4: 24 "Hyperkugeln" um eine 25.
Die überaus interessante und verblüffende Übereinstimmung zur christlichen Mystik:
Dimension 1: Die Trinität Gottes. Der dreieinige Gott: Vater, Sohn und heiliger Geist.
Ergo: Sohn und heiliger Geist "küssen" Gott.
Die Primzahl 3 schafft gemäß dem Sieb des Eratosthenes den 6er- Takt der Primzahlzwillinge.
Dimension 2: In 6 Tagen schuf Gott die Welt, am 7. Tage ruhte er (Genesis).
Ergo: Die 6 Schöpfungstage "küssen" Gott.
Die Primzahl 7 ist eine "göttliche Zahl". Die sieben Wochentage und der Sonntag als der "Tag des Herrn". Das dritte Gebot: "Du sollst den Feiertag heiligen", ruhen, nicht arbeiten...
|
|
Dimension 3: Die 12 Jünger um Jesus
herum. Jesus ist der 13.
Ergo: Die 12 Jünger "küssen" Jesus.
Die Primzahl 13 steht symbolisch für
Transformation. Die Überwindung
des Todes. Jesus als Todesüberwinder.
Dimension 4: Die 24 Ältesten um den Thron Gottes, der 25. (25, Quersumme 7) in der Apokalypse, bzw. Offenbarung Johannes.
Ergo: Die 24 Ältesten "küssen" Gott.
Der 24. als Weihnachtsfest. Der 25. als erster Weihnachtsfeiertag. Der Mensch gewordene Gott tritt in die Materie ein.
Die 25 ist keine Primzahl mehr, sondern das Vielfache von 5, also 5 x 5.
Primzahlen sind nur durch sich selbst und durch
1 teilbar. Somit sind sie ein Symbol der Einheit
und Abbild Gottes.
Die (Prim)Zahlen 1 x 2 x 3 schaffen mit dem 6er-Takt der Zwillingsbildung die "Göttliche Ordnung".
Die Ziffer 5 "zerstört" diese strenge "kristalline" Ordnung wieder und schafft mit ihrer Kombinatorik "Variantenreichtum".
Das Pentagramm = Goldener Schnitt.
Der Goldene Schnitt = Prinzip des Lebens.
Die Ziffer 5 = Zahl des Menschen (Leben).
|
|
Wie man also unschwer erkennen kann,
haben wir hier wieder eine Tetraktys, diesmal
tatsächlich auch mit vier Dimensionen:
1 + 2 + 3 + 4 = 10
Man beachte dabei auch das Kubooktaeder wie oben gezeigt:
6 + 6 + 6 + 6 = 24, bzw.:
1 x 2 x 3 x 4 = 24
Entsprechend den vier 6er-Takten der Primzahlzwillingsbildung bis zur 24.
Die vierte Dimension entspricht also sowohl dem Eintritt in den "transzendenten Raum" als auch der "Materialisierung" bzw. Manifestation der geistigen Prinzipien.
Der Kabbalist kennt diese Entsprechung:
Malchut ist Kether und Kether ist Malchut.
Gott offenbart sich in der Materie,
die Materie offenbart Gott.
Weitere interessante Zusammenhänge
zur Zahlenmystik in der christlichen Religionsphilosophie finden Sie unter:
WEIHNACHTEN, DER THRON GOTTES
UND DIE ZAHL 24
Weitere interessante Zusammenhänge zur Ziffer 24 finden Sie unter:
BEMERKENSWERTES ZUR ZAHL 24
^ Zurück nach oben^
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|