|
|
|
|
|
|
|
|
|
|
|
Welche Geometrie vermag Zahlen besser zu präsentiern als Polygone, deren Ecken den natürlichen Zahlen entsprechen?
Nun, es gibt tatsächlich eine Geometrie, die es noch besser kann: Es ist die Geometrie der Simplexe! Dabei handelt es sich
mathematisch gesehen um
Multidimensionale Tetraeder.
Simplexe sind Polygone, bei denen alle Eckpunkte diagonal mit jedem anderen Eckpunkt verbunden sind. Dabei entstehen innerhalb des Polygons Sternpolygone.
Diese Sternpolygone beschreiben geometrisch die Teilbarkeit der Eckenanzahl des
Polygons = natürliche Zahl.
|
Damit sind Simplexe sozusagen "Der feste Aggregatzustand der Zahl" oder "Die geometrische Fleischwerdung der Zahlen" ;-)
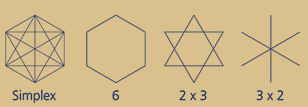
Beispiel:
Die 6 ist teilbar durch die 2 und die 3.
Das entsprechende Simplex enthält:
2 Dreiecke = 2 x 3 und 3 Linien = 3 x 2
|
Und das kann man durchaus wörtlich nehmen. Diese Geometrie gibt uns Orientierung, denn um Zahlen zu untersuchen, muss man
ein Zählsystem, wie zB. unser Dezimalsystem annehmen. Streng symmetrische Geometrie wie Polygon und Simplex aber ist universell,
sie "rechnet" nicht innerhalb eines
Zählsystems, und befreit uns deshalb von
entsprechenden Denkbarrieren.
Das Erstaunliche ist nun allerdings, dass die
Geometrie der Simplex dezimalcodiert ist!
Diese Tatsache zu untersuchen, ist ein
Hauptanliegen dieser Internetseite und
Gegenstand nachfolgender Betrachtungen.
|
|
 |
|
 |
|
 |
|
|
|
|
|
|
Gerade und ungerade Zahlen:
Es gibt ein signifikantes Unterscheidungs-
merkmal zwischen dem Simplex einer geraden
und einer ungeraden Zahl:
Nur bei geraden Zahlen führen Tangenten direkt durch den Mittelpunkt des Kreises
(des Polygons)! Denn die Konstellation der
Tangenten durch den Mittelpunkt beschreibt die
Tatsache: n/x = 2.
Eine Diagonale durch den Mittelpunkt = Linie,
welche aus einer Verbindung von zwei Punkten
besteht, ist identisch mit der Zahl 2.
Der Mengenstrahl enthält also eine stringente Drehmatrix und zeigt die exakten Teilereigenschaften an Hand einfacher geometrischer Figuren. |
|
|
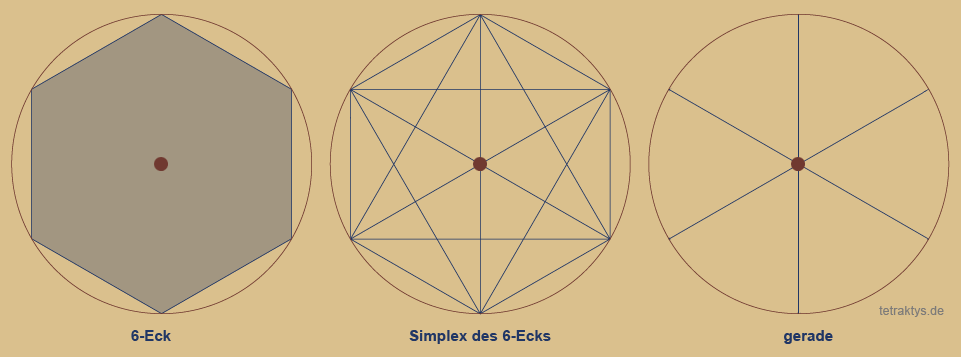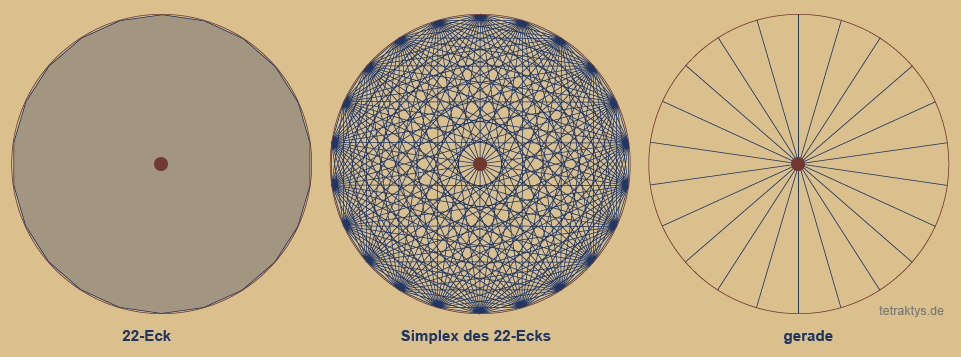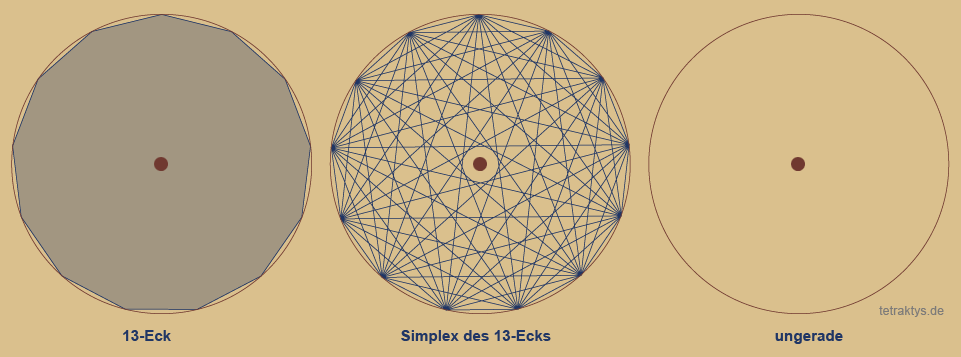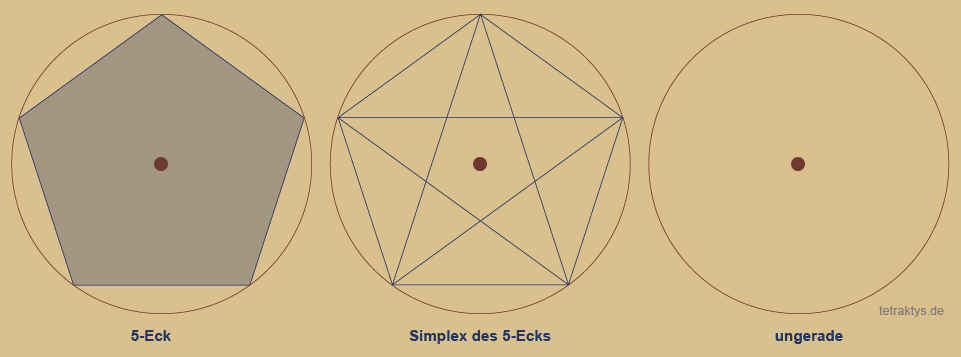
Polygone und natürliche Zahlen:
Das Spiel beginnt mit einem Punkt in der Mitte eines Kreises, welcher die Zahl 1 präsentiert.
Mit der Zahl 2 entsteht eine Linie, deren Enden
die Peripherie des Kreises markieren.
Die Zahl 3 ist die erste Zahl, die eine Fläche
mit entsprechenden Innenwinkeln aufspannt.
Die Zahl 4 ist die erste Zahl, in deren Polygon
sich Diagonalen einzeichnen lassen.
Wenn man ausgehend von Punkt, Gerade und Fläche die entsprechenden Dimensionssprünge weiter denkt, so kommen wir bei der Ziffer 4 auf die 3. Dimension!
Demnach sind die Diagonalen im 4-Eck gleich einem Tetraeder auf eine beliebige Kante geschaut.
Siehe:
Multidimensionale Tetraeder.
|
Simplexe und natürliche Zahlen:
Hier sehen Sie nun zeitgleich die Entsprechung
des jeweiligen Polygons als Simplex. Jeder
Eckpunkt ist mit jedem anderen möglichen
Eckpunkt verbunden. Dabei entstehen um so
mehr Diagonalen quer durch das Polygon,
je größer die Anzahl seiner Ecken ist.
Jede hinzukommende Ecke stellt einen Dimensionssprung dar. Siehe auch: Multidimensionale Tetraeder, hier soll es im Folgenden um den zahlentheoretischen Hintergrund gehen.
Auf dem ersten Blick mutet dieses System chaotisch an. Denkt man es jedoch ausgehend
vom Polygon konsequent von außen nach innen
weiter, erkennt man eine strenge Ordnung.
Nachfolgend versuche ich zu illustrieren, wie diese Ordnung funktioniert...
|
|
 |
|
|
 |
|
|
|
|
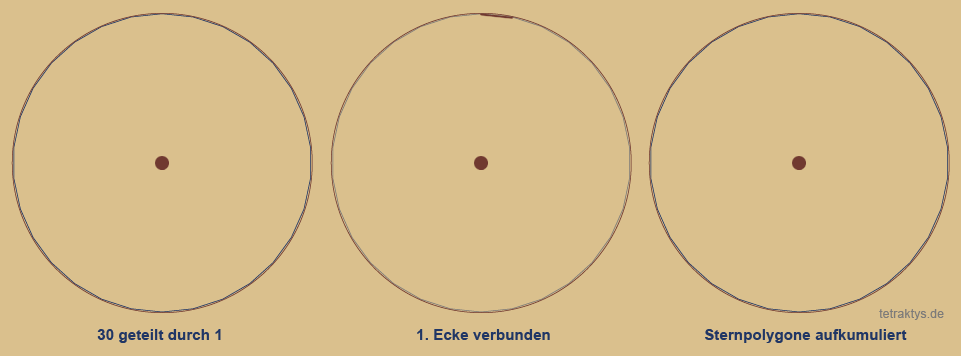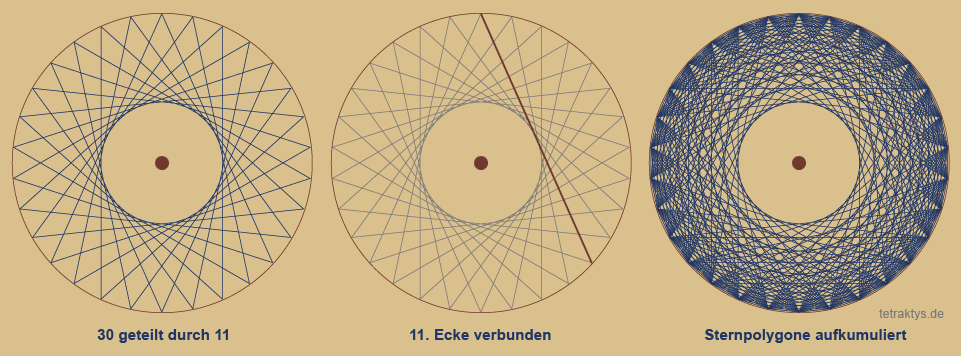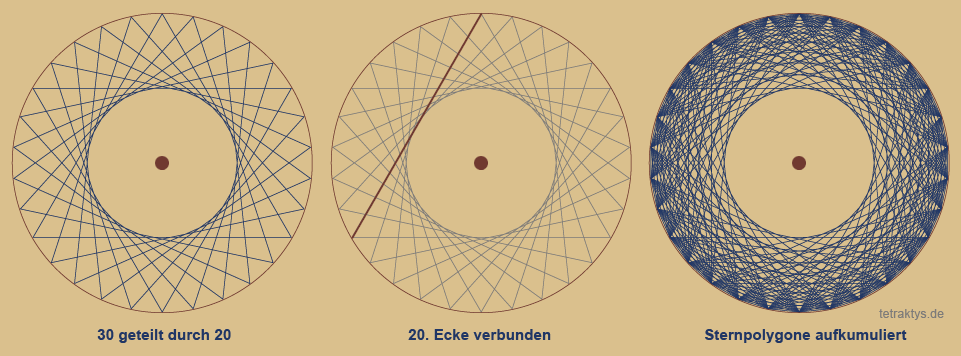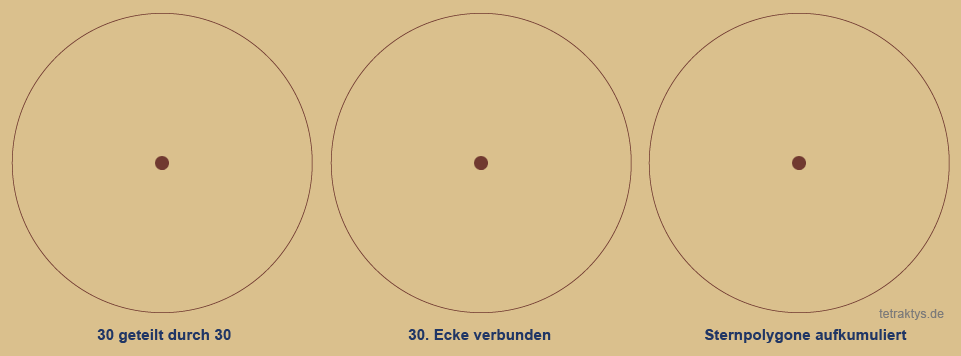
Simplexaufbau am Beispiel der Ziffer 30:
Um zu demonstrieren, wie ein Simplex aufgebaut ist, empfielt es sich, solch eine Figur mit einer genügend große Eckenanzahl zu wählen, in diesem Fall ein 30-Eck-Simplex.
So kann man erkennen, dass die Mehrfachüberschneidungen der einzelnen Sternpolygone Vierecke ergeben.
Es handelt sich dabei quasi um ein Koordinatensystem innerhalb der Geometrie des Kreises. Einzelheiten dazu später.
Jedes Sternpolygon innerhalb eines Simplex
(hier am Beispiel des 30-Ecks sind es 15)
zeigt eine Teilbarkeitskonstellation an.
Ab der Ziffer 16 bis 30 muss das System revers laufen, denn die Linie durch den Mittelpunkt beschreibt in diesem Beispiel:
30 geteilt durch 15 = 2
|
|
Teilbarkeit natürlicher Zahlen und Prinzip
der geometrischen Entsprechung:
Als Ausgangspunkt (Drehpunkt) wurde eine beliebige Ecke gewählt, um das Prinzip anschaulich zu machen.
Die rote Linie muss also als ein Teil des jeweiligen Sternpolygons verstanden werden.
Jede Ecke verbunden:
30 geteilt durch 1. Dies erfordert einen Umlauf,
also das 30-Eck selbst.
Jede 2. Ecke verbunden:
30 geteilt durch 2. Dies erfordert zwei Umläufe
bis alle Ecken verbunden sind = erstes Sternpolygon
Jede 3. Ecke verbunden:
30 geteilt durch 3. Dies erfordert drei Umläufe
bis alle Ecken verbunden sind = zweites Sternpolygon... u.s.w....
|
|
Sternpolygone aufkumuliert:
Dies Darstellung habe ich gewählt, um zu zeigen, wie die einzelnen übereinander gelagerten Sternpolygone, dieses typische Muster eines größeren Simplex ergeben.
Zwar ist bei einem Simplex prinzipiell jede Ecke mit jeder anderen verbunden, jedoch muss man diese Geometrie symmetrisch denken, um das System dahinter zu verstehen.
Diese Einzelheiten vom Aufbau eines Simplex sind wichtig, um die vier Hauptgruppen
von Polygonen bzw. Sternpolygonen und ihre zahlentheoretische Entsprechung
zu verstehen.
Das Wissen um die nun folgenden
Zusammenhänge sind für das Verständnis
der Pythagoreischen Tetraktys von größter Bedeutung!
|
|
|
|
|
 |
|
1. Polygon (Polygone in einem Zug gezeichnet)
Diese Konstellation beschreibt: Alle natürlichen Zahlen ohne Teiler. Hier handelt es sich ganz einfach um die jeweiligen Polygone entsprechend den natürlichen Zahlen, weshalb man Polygone auch als n-Ecke bezeichnet.
Die ersten n-Ecke sind: Punkt, Linie, Dreieck, Viereck, Fünfeck, Sechseck u.s.w.... Das erste Polygon ist das Dreieck! |
|
 |
|
|
2. Sternpolygon (Sternpolygone in einem Zug gezeichnet)
Diese Konstellation beschreibt: Natürliche Zahl, ist mit dem betreffenden Teiler teilerfremd, bzw. relativ prim. Simplexe, deren Eckenanzahl prim ist (mit Ausnahme der Zahl 2 und 3) setzen sich prinzipiell nur aus Sternpolygonen zusammen, die in einem Zuge gezeichnet werden können. |
|
|
|
|
 |
|
|
|
|
 |
|
 |
|
|
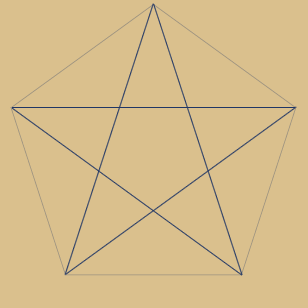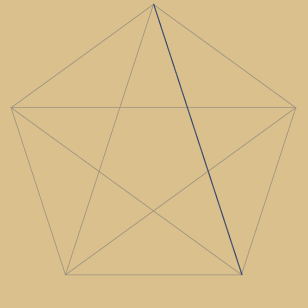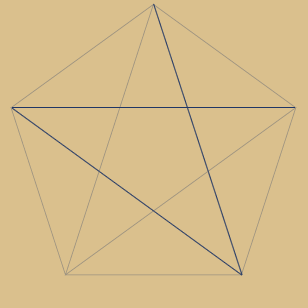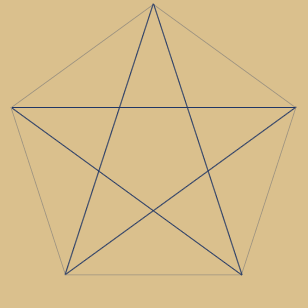
Beispiel Primzahl 5 – also 5-Eck-Simplex
Das Pentagramm im Fünfeck ist
das prominenteste Beispiel dieses Simplex-Typs
und zugleich auch der erste
Sternpolygon-Typ dieser Art!
Jede 2. Ecke wird verbunden, bis alle
5 Ecken erfasst sind. Dies entspricht:
5 / 2 = 2,5
Die Primzahlen 2 und 3 sind ein Sonderfall. Zwar werden eine Linie (2) und ein Dreieck (3) auch in einem Zug gezeichnet, aber es handelt sich dabei nicht um Sternpolygone! Diese Unterscheidung ist wichtig, um das System zu verstehen.
Schauen Sie sich hier die überaus wichtige zahlentheoretische Entsprechung dazu an!
|
|
|
|
|
|
|
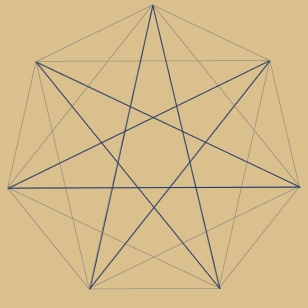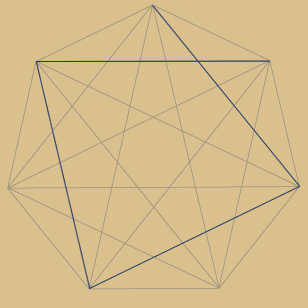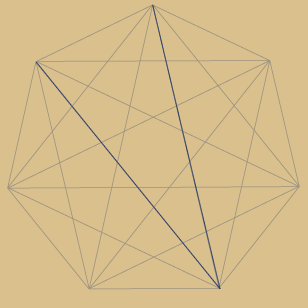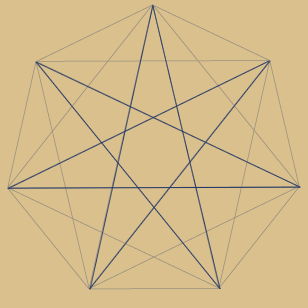
Beispiel Primzahl 7 – also 7-Eck-Simplex
Hier haben wir zum ersten Mal gleich zwei
dieser Konstellationen innerhalb eines n-Ecks!
Und Achtung:
hier wird es etwas kompliziert, denn man
darf diese Konstellation nicht mit der zuletzt
beschriebenen 4. Gruppe verwechseln, also bitte genau hinschauen und verstehen!
Jede 2. Ecke wird verbunden, bis alle 7 Ecken
erfasst sind. Dies entspricht:
7 / 2 = 3,5
Jede 3. Ecke wird verbunden, bis alle 7 Ecken
erfasst sind. Dies entspricht:
7 / 3 = 2,333...
|
Ein Beispiel am 30-Eck-Simplex
Die Ziffer 30 ist natürlich keine Primzahl,
Allerdings gibt es ab der Ziffer 7 in jeder
Zahl teilerfremde bzw. relativ prime Teilbarkeitskonstellationen, so auch im 30-Eck.
Hier in diesem Beispiel wird jede 11. Ecke verbunden, bis alle 30 Ecken erfasst sind.
Dies entspricht:
30 / 11 = 2,72....
Interessant dabei:
Trotz der unregelmäßigen Tangentenabstände
beim Aufbau: Es wird konsequent jede 11. Ecke
verbunden, das Ergebnis ist perfekte Symmetrie!
|
|
 |
|
|
3. Polygon mehrfach (Sternpolygone, bestehend aus mehreren Polygonen)
Alle Simplexe, deren Anzahl der Ecken nicht prim ist, beinhalten Sternpolygone, die sich aus mehreren Polygonen zusammensetzen.
Diese Konstellation beschreibt: Natürliche Zahl, ist mit dem betreffenden Teiler teilbar.
|
|
|
|
|
 |
|
|
 |
|
|
 |
|
|
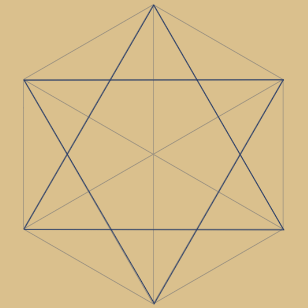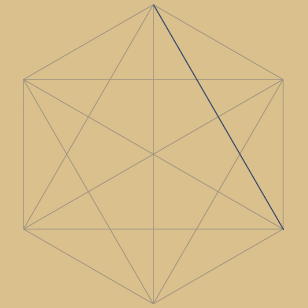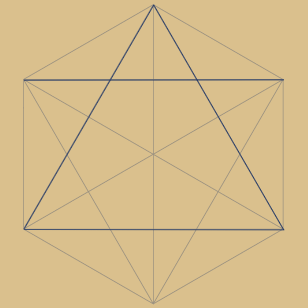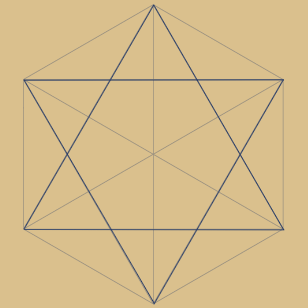
Der Sechsstern bzw. das Hexagramm ist
das prominenteste Beispiel und zugleich auch
der erste Sternpolygon-Typ dieser Art.
Jede 2. Ecke wird verbunden, bis alle 6 Ecken erfasst sind. Das Ergebnis sind zwei Dreiecke.
Dies entspricht: 6 / 2 = 3
Zwar ergeben zwei Punkte = 2 / 2 = 1 und zwei Linien = 4 / 2 = 2 ebenfalls eine teilbare Konstellation , aber es handelt sich dabei nicht um Polygone. Diese Unterscheidung ist wichtig, um das System zu verstehen.
|
|
Im 8-Eck befindet sich die zweite Konstellation dieser Art. Jede 2. Ecke wird verbunden, bis alle 8 Ecken erfasst sind. Das Ergebnis sind 2 Quadrate.
Dies entspricht: 8 / 2 = 4
|
|
Ein Beispiel am 30-Eck zeigt diesen Typ eines Sternpolygons mit einer größeren Eckenanzahl.
Hier mit 10 Dreiecken. Jede 10. Ecke wird verbunden, bis alle 30 Ecken erfasst sind.
Dies entspricht: 30 / 10 = 3.
|
|
|
 |
|
|
4. Sternpolygon mehrfach (Sternpolygone, bestehend aus mehreren Sternpolygonen)
Alle Simplexe ab der Ziffer 10, deren Anzahl der Ecken nicht prim ist, beinhalten Sternpolygone, die sich aus mehreren Sternpolygonen zusammensetzen
(einzige Ausnahme ist jedoch das 12-Eck). Diese Konstellation beschreibt: Natürliche Zahl, ist mit dem betreffenden Teiler nicht teilbar, hat aber mit ihm mindestens einen gemeinsamen Teiler größer als eins.
|
|
|
|
|
 |
|
 |
|
 |
|
|
Die erste Konstellation dieser Art befindet
sich im 10-Eck, es setzt sich aus zwei
Pentagrammen zusammen.
Jede 4. Ecke wird verbunden, bis alle 10 Ecken erfasst sind. Dies entspricht:
10 / 4 = 2,5
Gemeinsamer Teiler von 10 und 4 ist die 2.
|
|
Im 14-Eck befindet sich die nächste Konstellation dieser Art. Diese setzt sich aus zwei Heptagrammen (Siebensternen) zusammen, die sich jeweils in einem Zug zeichnen lassen. Jede 4. Ecke wird verbunden, bis alle 14 Ecken erfasst sind. Dies entspricht: 14 / 4 = 3,5
Gemeinsamer Teiler von 14 und 4 ist die 2.
|
|
Ein Beispiel am 30-Eck zeigt diesen Typ eines Sternpolygons mit einer größeren Eckenanzahl.
Hier mit 6 Pentagrammen. Jede 12. Ecke wird verbunden, bis alle 30 Ecken erfasst sind.
Dies entspricht: 30 / 12 = 2,5
Gemeinsame Teiler von 30 und 12 sind 6, 3 und 2. |
|
|
 |
|
|
Auffächerung der Sternpolygone in ein Koordinatensystem bzw. in das Lambdoma
|
|
 |
|
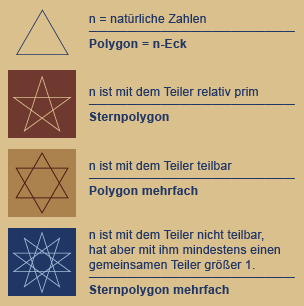
Nachdem wir die vier geometrischen Grundtypen entsprechend den drei möglichen Teilbarkeiten natürlicher Zahlen herausgearbeitet haben, die in einem beliebigen n-Simplex vorkommen bzw. vorkommen können, wollen wir nun sehen, wie sie sich innerhalb eines Koordinatensystems verteilen, und welche Gesetzmäßigkeiten dabei auftreten.
Auf der linken Seite sehen wir die Legende zu darunter stehendem Koordinatensystem. Es sind hier auch genau jene Figuren dargestellt, mit denen das jeweilige Prinzip beginnt!
Die drei Teilbarkeitskonstellationen sind entsprechend gefärbt, um sie dem System zuordnen zu können.
Was zeigt das Koordinatensystem?
In der obersten Reihe sehen wir die kompletten Simplexe von 1 bis 14, direkt darunter ihre Auffächerung, beginnend von der Peripherie des
|
|
Kreises – also das Polygon – bis zu den Linien durch den Mittelpunkt bei geraden Zahlen!
Die vertikale Spalte links zeigt die jeweiligen Teiler
an! Beispiel: Das erste Sternpolygon, das sich in
einem Zug zeichnen lässt, ist das Pentagramm.
Es präsentiert die Teilbarkeitskonstellation:
5 geteilt durch 2!
An dieser Stelle muss ich unbedingt auf eine Sache hinweisen, die zu Missverständnissen führen kann, nämlich der Begriff "Sternpolygon"!
Jene Figur, die ich als "Polygon mehrfach" bezeichne, könnte man ebenfalls "Sternpolygon" nennen, und es ist durchaus ein Sternpolygon, nur eben eines, das sich aus Polygonen zusammensetzt!
Um diesen Missverständnissen aus dem Wege
zu gehen, halte man sich einfach an die farbliche
Kennzeichnung, dann ist man auch auf der
sicheren Seite!
|
|
|
 |
|
|
|
|
|
 |
|
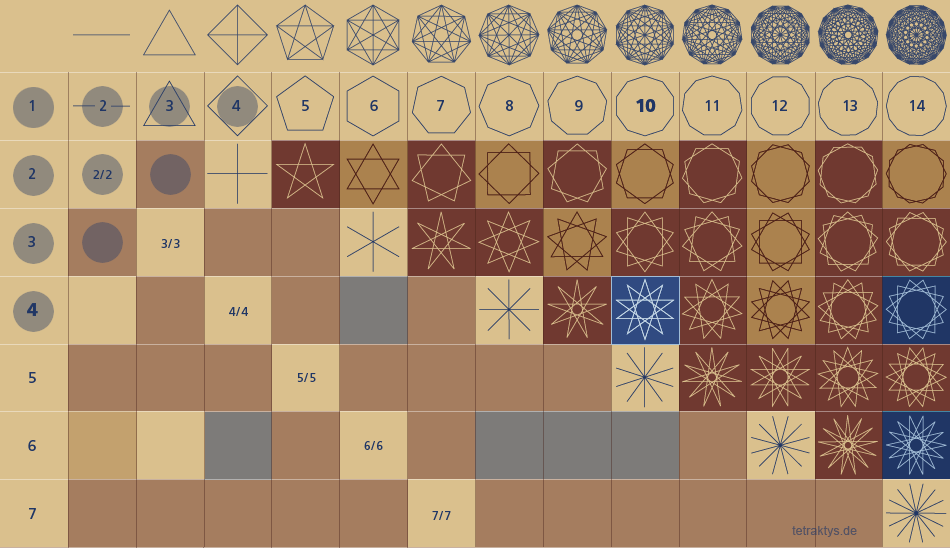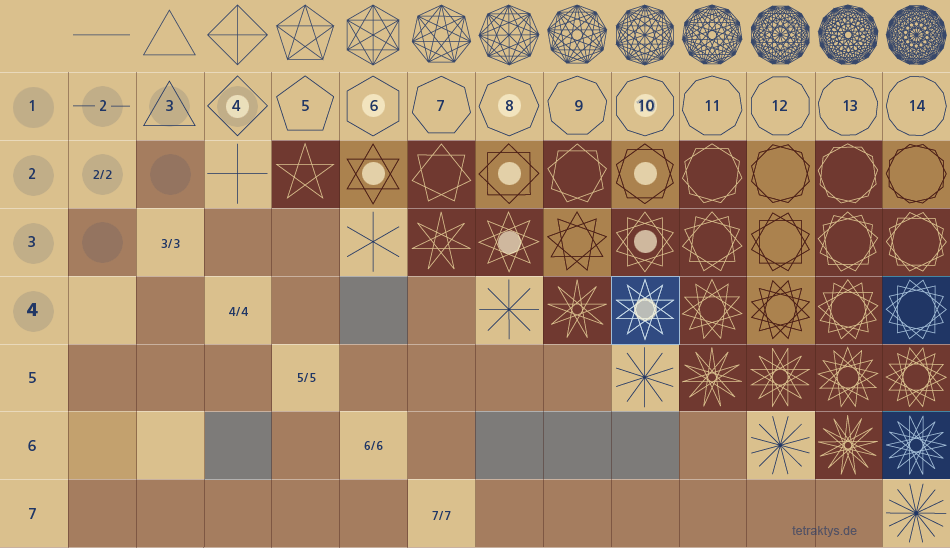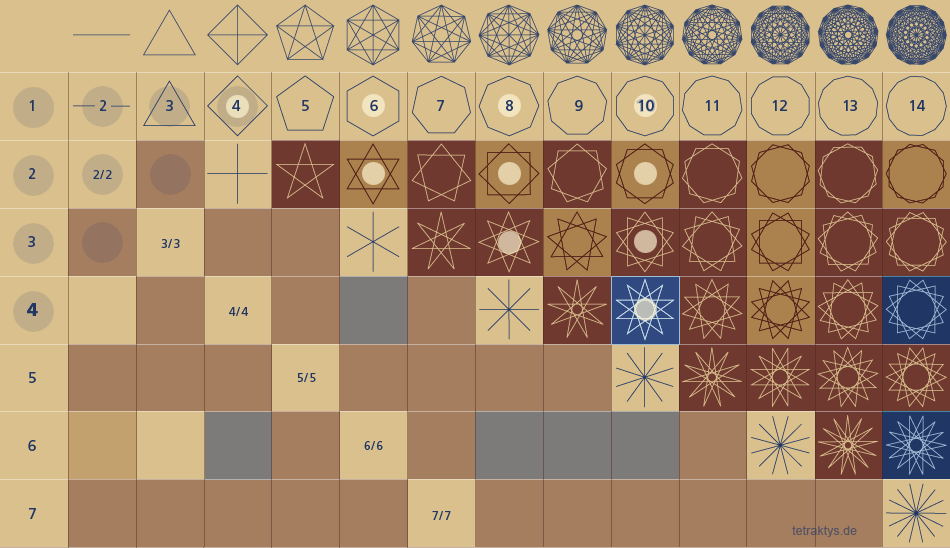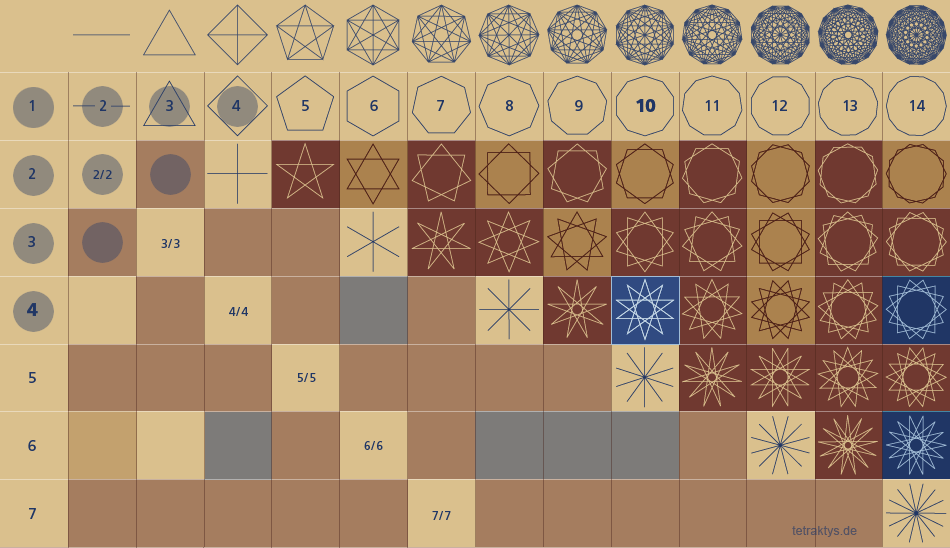
Um den vorerst wichtigsten Tatbestand auf sich wirken zu lassen, habe ich obige Grafik noch einmal stark verkleinert in quadratischen Kantenlängen dargestellt und um 45 Grad gekippt, um die ihm innewohnende Symmetrie anschaulich
zu machen.
Genau so wird auch das so genannte Lambdoma
in der Harmonik dargestellt. Mehr noch:
Es ist das Lambdoma der Harmonik, das
wichtigste Diagramm in der Musiktheorie!
Auch empfand ich es als sinnvoll, hier eine größere Anzahl "Pixel" (also Simplexe bzw. Sternpolygone!) für die Veranschaulichung eines Sachverhalts zu verwenden. Was möchte ich zeigen?
Die gesamte Geometrie der Simplexe wurde aufgefächert. Auffällig ist aber, dass nur der vierte Teil des gesamten Koordinatensystems mit Geometrie gefüllt ist!
Was limitiert diese Grenze?
Alle geradzahligen Simplexe schließen mit
entsprechenden Linien durch den Mittelpunkt des
Kreises ab!
Dieser "Linienstern" am Ende der
Auffächerung hat immer das Teilbarkeits-
ergebnis 2! Beginnend mit der Ziffer 2, bei der
es sich ja ebenfalls um eine Linie handelt.
Natürlich könnten wir das komplette System mit
Geometrie füllen, so dass sich die Sternpolygone
in ihrer Reihenfolge wiederholen.
Darauf kommen wir später noch zurück, denn wir müssen selbstverständlich auch untersuchen, welche Entsprechung es in diesem Fall zur Zahlentheorie gibt.
|
|
|
|
|
Danach bauen sich die Sternpolygone
in Moduloform auf, dazu später mehr.
Und tatsächlich beschreibt auch die Zeugertonlinie des harmonikalen Lambdomas die Ziffer 1, da
selbstverständlich auch hier immer die selben
Zahlen des Koordinatensystems aufeinader
treffen! ( 1/1, 2/2, 3/3, 4/4 usw....)
Hier muss man sich wieder die Frage stellen:
Was hat diese 4-Teilung allein aus der
Kreisgeometrie heraus ( ! ) möglicherweise mit
der Pythagoreischen Tetraktys (Vierheit) zu tun?
Was immer sich derjenige darunter vorstellen mag,
der geneigt ist diese Frage zu belächeln.
Diese Thematik ist für die Zahlentheorie
von größter Bedeutung.
Denn:
Alle Teilbarkeitskonstellationen natürlicher
Zahlen sind unterhalb der "Schranke 2"
für die Primzahlproblematik nicht mehr
relevant, da ja ab hier die jeweilige natürliche
Zahl ohnehin nicht mehr in mindestens zwei
natürliche Zahlen größer 1 geteilt werden
kann.
Die beige-gelb gefärbten Pixel im Lambdoma
zeigen diesen Sachverhalt. Nur diese Pixel
sind mit Sternpolygonen besetzt, welche sich
aus Polygonen zusammensetzen.
Nur diese beschreiben:
n ist mit dem Teiler teilbar.
Und an dieser Stelle möchte ich einfach mal
darauf hinweisen, dass die Kreisgeometrie
(Kreiszahl Pi) in der Riemannschen Zetafunktion
durchaus eine wichtige Rolle spielt. Bis heute
gibt es keine plausible Erklärung dazu.
|
|
 |
|
Nun ist es aber erst einmal wichtig,
sich folgendes vor Augen zu halten:
Es ist der Mittelpunkt des Kreises der das Limit setzt! Es ist die Schranke der Ziffer 2, die Linie durch den Mittelpunkt des Kreises, welche den Kreis in genau zwei Teile teilt, die aber auf das Koordinatensystem bezogen, genau ein Viertel des Systems ausmacht!
Die Linie welche das Koordinatensystem
in der Mitte in zwei Teile teilt, beschreibt demnach eine volle Kreisumdrehung!
Denn nach der "Schranke 2", der Linie durch den Mittelpunkt des Kreises, läuft die selbe Geometrie noch einmal spiegelsymmetrisch ab, genau bis
zur Linie, die das Koordiantensystem in zwei
Teile teilt.
|
|
 |
|
|
Kommen wir nun zu jenem Sachverhalt,
der Kernthema dieser Internetseite ist,
die Dezimalcodierung im 4. Teil des Lambdomas ( 1 + 2 + 3 + 4 = 10 ) ! :
Wie an Hand obigen Geometrie-Tabelle
deutlich zu erkennen ist, beginnt die dritte
Teilbarkeitskonstellation:
"Natürliche Zahl, ist mit dem betreffenden
Teiler nicht teilbar, hat aber mit ihm
mindestens einen gemeinsamen Teiler
größer als eins."
oberhalb der "Schranke 2" genau mit der
Ziffer 10 und dem Teiler 4.
Genauer gesagt:
10 geteilt durch 4 = 2,5 !!!
Man sollte noch besser sagen:
"Zwei und ein Halbes!"
Das Pentagramm selbst und alle Sternpolygone die aus Pentagrammen zusammengesetzt sind, entsprechen immer zwei Ganzen und einem Halben – also dem Verhältnis von 4 zu 1!
Hier wird dieser Sachverhalt deutlicher vor Augen führt:
DER SCHLÜSSEL ZUR TETRAKTYS
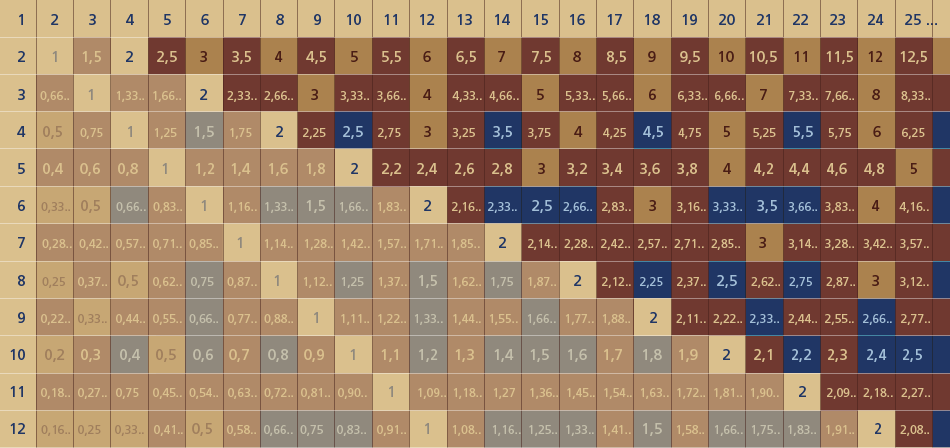
Die unten stehende Tabelle zeigt statt der
oben dargestellten Auffächerung der
Simplexe in Sternpolygone nun die
|
|
entsprechenden Teilbarkeitsergebnisse
zu den jeweiligen X-Y-Positionen
der Sternpolygone.
Wie weiter oben schon bemerkt, ist dieses System auch identisch mit dem
Lambdoma der Harmonik, nur mit dem
Unterschied, dass statt der Zahlenbrüche
hier eben schon die Ergebnisse dieser
Brüche eingetragen wurden.
Zu dieser Tabelle gäbe es eine Menge zu sagen. Man schaue sie sich einfach erst mal in Ruhe an.
Aus grafischen Gründen habe ich hier eine Ansicht mit relativ wenigen Zahlen (bis 25) gewählt, da sonst die eingetragenen Zahlen der Teilbarkeitsergebnisse der entsprechenden Sternpolygone nicht mehr lesbar wären.
Eine Ansicht mit komplett eingetragenden Werten der X-Y-Positionen ist aber notwendig, um den Bezug zur entsprechenden Geometrie herstellen
zu können.
Den Bereich unterhalb der "Schranke 2" birgt eine extra Überraschung und stellt deshalb auch ein extra Thema dar.
Weiter geht es mit der Primzahlproblematik und den Simplexen in der Rubrik "Zahlentheorie", und da in:
DIVISIONSTABELLE & SIEB DES ERATOSTHENES
|
|
Aus diesen Tabellen ist dann jene
Dezimalkodierung ersichtlich, die sich
zwangsläufig aus dieser hier darstellten
Tatsache ergeben muss.
Und es handelt sich dabei immmer um die
entsprechende Geometrie der Simplexe.
Diese wurden bis zum 100-Eck-Simplex
gezeichnet und untersucht.
"Hier mag der Berufsmathematiker
einwenden:
Für eine Beweisführung zur Problematik der
Primzahlverteilung sind Zahlenmengen
bis 100 absolut undiskutabel!"
Nun:
Diese Geometrie ist mit dem Sieb des Eratosthenes absolut deckungsgleich,
weshalb Tabellen bis 100 völlig ausreichend
sind, um den Sachverhalt eindrucksvoll zu
demonstrieren.
Denn bekanntermaßen ist das Sieb bis in den unendlichen Zahlenraum hinein gültig!
|
|
|
 |
|
|
^ Zurück nach oben ^
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|