|
|
|
 |
|
|
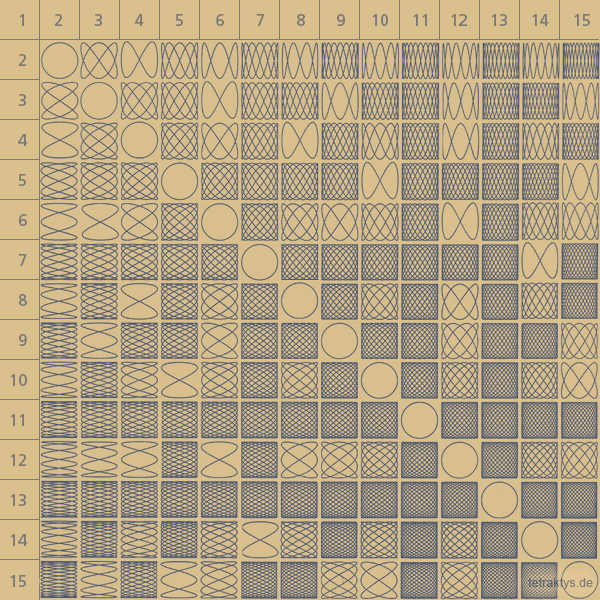
Das Lambdoma zeigt ein 45 Grad gekipptes
Koordinatensystem, deren x- und y-Achse jeweils
die Zahlengerade bis unendlich enthalten.
Die einzelnen Positionen innerhalb des
Koordinatensystems zeigen die daraus
resultierenden, jeweiligen Zahlenbrüche.
Die namensgebende dreieckförmige Darstellung
des Lambdomas (benannt nach dem griechischen
Buchstaben Lambda) soll die ihm innewohnende
Symmetrie anschaulich machen.
Hier finden Sie Einzelheiten zum Lambdoma aus der Sicht der Harmonik und der Musiktheorie:
DAS LAMBDOMA – HARMONIK & TETRAKTYS
Dieser Link betrachtet das Lambdoma aus rein zahlentheoretischer Sicht:
DAS LAMBDOMA IN DER ZAHLENTHEORIE
Im Folgenden nun einige Entsprechungen dieser
Matrix nicht nur in der abstrakten Welt der
Zahlen und der Symmetrien, sondern in
unserer erfahrbaren Welt – in der Physik.
|
|
|
|
 |
|
|
Harmonische Schwingungen
und ihre Anordnung im Lambdoma
Das Grundprinzip des Lambdomas in der Musiktheorie ist es, zwei Töne im rechten Winkel
miteinander reagieren zu lassen.
Zeichnen wir nun die Formen auf, die entstehen, wenn sich zwei Schwingungen begegnen, dann erhalten wir sogenannte Lissajousfiguren. Siehe dazu die Abbildung rechts.
Hier nun ist das Koordinatensystem zur besseren
Darstellung der Lissajousfiguren wieder in üblicher Form dargestellt (nicht 45 Grad gekippt).
Zwei Töne gleicher Frequenz, die sich im rechten Winkel begegnen, ergeben bei entsprechender Phasenlage einen Kreis.
Hier ein Link zu einer Seite, auf der man den Lissajousfiguren die entsprechenden musikalischen Intervalle zuordnen kann:
http://gerdbreitenbach.de/lissajous/lissajous.html
Dies entspricht auch der vollen
Kreisumdrehung in der Geometrie
der Polygone und Sternpolygone
innerhalb des Lambdomas !
Siehe dazu:
SIMPLEX – DER FESTE
AGGREGATZUSTAND DER ZAHL
Wenn man nun das Lamdoma mit den Lissajousfiguren über das Zahlenlambdoma legt, dann kann man sehen, dass spezifische Wellenformen in ihrer x-y-Postion exakt mit der entsprechenden zahlentheoretischen und geometrischen Aussage übereinstimmen!
Besonders faszinierend die jeweiligen Wellenformen mit ihren entsprechenden Überschneidungen.
|
|
|
|
 |
|
|
|
 |
|
|
 |
|
|
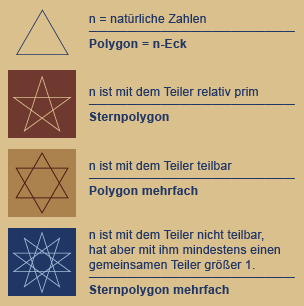
Im Folgenden noch einmal die zahlentheoretische und geometrische Entsprechung der Farbcodierung:
|
|
|
|
 |
|
|
|
Hier stoßen wir nun aber auf ein Problem, auf welches ich schon mehrmals hinwies, und welches auch für die Dezimalcodierung, eben der Tetraktys (1+2+3+4=10) verantworlich ist:
Die Geometrie der Sternpolygone ist in der oben dargestellten Charakteristik nur genau bis zu einem Viertel mit den Zahlenwerten identisch, nämlich bis zum Teibarkeitsergebnis 2.
Interessanterweise reicht aber genau dieses Viertel Geometrie um das Primzahlverteilungsproblem anschaulich zu machen, denn die Primzahlproblematik ist nur oberhalb der "Schranke 2" relevant! Näheres dazu ebenfalls unter:
SIMPLEX – DER FESTE
AGGREGATZUSTAND DER ZAHL
|
|
|
|
 |
|
|
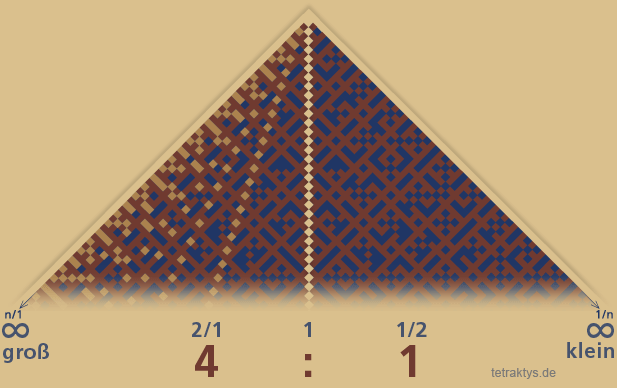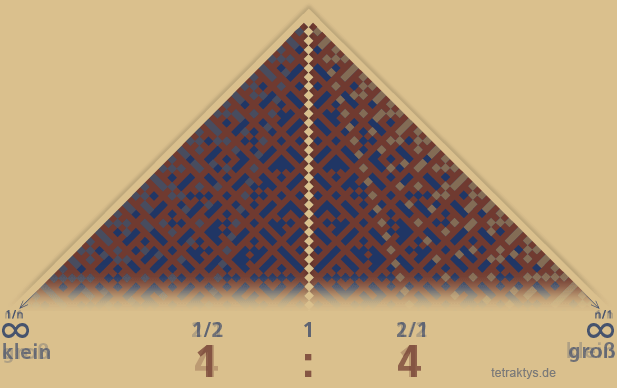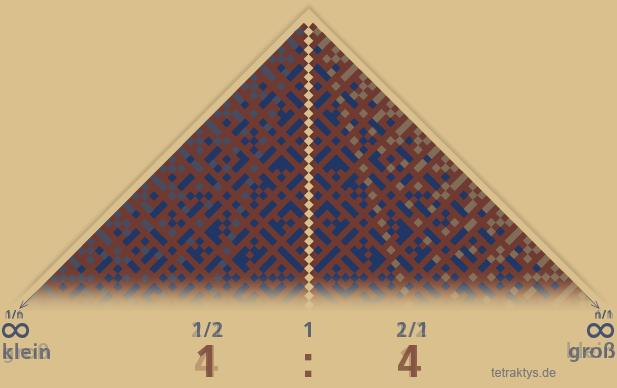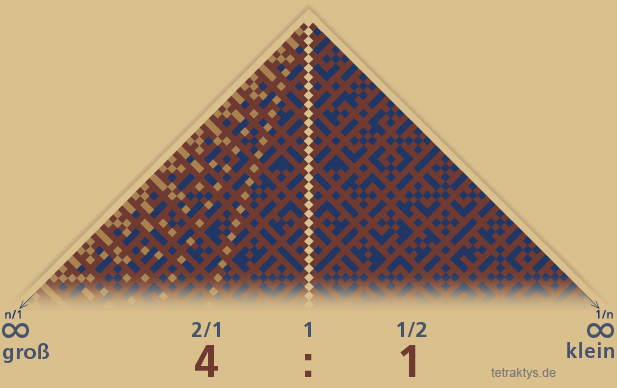
Allerdings ist es auch eine Frage der Betrachtungsweise, denn man kann prinzipiell
die beiden Zahlengeraden von Zähler und Nenner beliebig vertauschen, womit die reziproken Werte der einen Hälfte des Lambdomas mit der anderen Hälfte ebenfalls vertauscht sind.
Was sich dabei ändert, sind lediglich die teilbaren Konstellationen:
"n ist mit dem Teiler teilbar" (beigegelb).
diese werden ersetzt durch: "n ist mit dem Teiler nicht teilbar, hat aber mindestens einen gemeinsamen Teiler größer 1" (dunkelblau).
Hier noch einmal die Farblegende:
|
|
|
|
 |
|
|
 |
|
|
|
Die Symmetrie bleibt also erhalten!
Um die Symmetrie des farblich gekennzeichneten "Matrixcodes" zu veranschaulichen, ist es wieder sinnvoll, das Lambdoma so darzustellen, dass es seinem Namen gerecht wird – in der üblichen dreieckigen Form, also um 45 Grad gekippt,
so wie die Grafik rechts es zeigt.
|
|
|
|
Eine weitere interessante Sichtweise:
Die dunkelblauen und beigegelben Felder zeigen sich wiederholende Zahlenbrüche an, die rotbraunen Felder dagegen zeigen neue Konstellationen an.
Im unendlich gedachten Lambdoma beträgt die Dichte der rotbraunen Felder gegenüber den restlichen Feldern 6 / pi hoch 2 !
Einzelheiten unter:
DAS LAMBDOMA – DIE MATRIX DER SCHÖPFUNG?
|
|
|
|
 |
|
|
Lichtwellen und ihre Anordnung
im Lambdoma
Leider habe ich noch keine Zeit gefunden, zu diesem Thema zu schreiben.
Ich werde mich aber bemühen, demnächst
zumindest ein paar einleitende und auch
erklärende Sätze zu diesem Thema
nachzuliefern!
|
|
|
|
|
|
|
|
 |
|
|
 |
|
|
|
 |
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|