|
|
|
|
|
|
|
|
|
|
|
Primzahlen, Teilbarkeit und die Zahl 24
Generalisierte Pentagonalzahlen
Man nehme eine Primzahl größer als 3,
multipliziere sie mit sich selbst und ziehe 1
davon ab.
Warum ist das Ergebnis immer
ohne Rest durch 24 teilbar?
Vermindert man das Quadrat einer Primzahl p
um 1, so kann auf das entstehende Ergebnis Z
die dritte binomische Formel angewendet werden
und Z lässt sich als Produkt von zwei Faktoren
in folgender Weise darstellen:
Z = p2 – 1 = (p – 1) · (p + 1)
Da nur Primzahlen p genommen werden dürfen,
die größer als 3 sind, muss p immer ungerade sein,
da die einzige gerade Primzahl die 2 ist.
Deshalb muss der erste Faktor (p – 1) gerade sein.
Z ist also immer ohne Rest durch 2 teilbar.
Ebenso muss auch der zweite Faktor (p + 1) gerade sein. Deshalb ist Z sogar ohne Rest
durch 4 teilbar.
Die Faktoren (p – 1) und (p + 1) sind benachbarte
gerade Zahlen. Da jede zweite gerade Zahl
durch 4 teilbar ist, muss einer der beiden
Faktoren durch 4, der andere durch 2 teilbar
sein. Das Ergebnis Z ist also sogar ohne Rest
durch 8 teilbar.
|
Die Zahlen (p – 1), p und (p + 1) folgen direkt
aufeinander. Von drei aufeinanderfolgenden Zahlen ist immer eine durch 3 teilbar.
Entsprechend der Aufgabe muss die Primzahl p aber größer als 3 sein und kann deshalb nicht durch 3 teilbar sein.
Dann muss einer der beiden verbleibenden Ausdrücke (p – 1) oder (p + 1) durch 3 teilbar sein. Da das Ergebnis Z das Produkt dieser beiden Ausdrücke ist, muss Z folglich auch durch 3
und deshalb insgesamt sogar ohne Rest
durch 24 teilbar sein.
Die kleinste Primzahl größer als 3 ist die 5.
Für sie ist Z = p2 – 1 = 24. Das bedeutet,
dass 24 auch die größte Zahl ist, durch die Z
immer ohne Rest geteilt werden kann.
Intuitiv glauben viele nicht, dass man aus
praktisch allen Primzahlen auf so einfache
Weise Zahlen erzeugen könne, die alle durch
die hochzusammengesetzte Zahl 24 teilbar sind.
Beispiele:
5 · 5 – 1 = 24 = 1 · 24
7 · 7 – 1 = 48 = 2 · 24
11 · 11 – 1 = 120 = 5 · 24
13 · 13 – 1 = 168 = 7 · 24
17 · 17 – 1 = 288 = 12 · 24
19 · 19 – 1 = 360 = 15 · 24 usw...
Dieser Text entstammt der Internetseite
vom Werner Brefeld:
Primzahlen, Teilbarkeit und die Zahl 24
|
Diese Zusammenhänge sind auch ein Kernthema von
Dr. Peter Plichtas Primzahlkreuz.
Ein weiterer interessanter Sachverhalt:
Bei den Zahlen: 1, 2, 5 ,7, 12, 15 usw.
handelt es sich um so genannte
Generalisierte Pentagonalzahlen:
n · (3 · n-1) / 2, n = 0, + - 1, + - 2
D.h.: Gruppe A die sog. Fünfeckszahlen
(Pentagonal numbers):
0, 1, 5, 12, 22, 35, 51....
und Gruppe B: die sog. Kartenhauszahlen
(Second pentagonal numbers):
0, 2, 7, 15, 26, 40, 57....
siehe dazu auch:
Generalized pentagonal numbers
In wieweit diese Pentagonalzahlen etwas
mit den hier dargestellten geometrisch
zahlentheoretischen Beziehungen zu den
Simplexen bzw. Sternpolygonen, und
insbesondere die Beziehung des
Pentagramms ( 2,5 · 10 = 25 ) zur
unregelmäßigen Primzahlverteilung
direkt nach der Ziffer 24 zu tun haben,
sollte untersucht werden!
Zur Erinnerung:
Die Ziffer 5 ist die erste Primzahl, die sich auf einem Primzahlzwillingsplatz der Form 6n ± 1 befindet! Die Ziffer 25 ( 5 · 5 ) ist die erste Pseudoprimzahl, die sich auf einem Primzahlzwillingsplatz der Form 6n ± 1 befindet, was mindestens geometrisch interessant ist!
|
|
 |
|
|
Pyramidenzahlen und die Zahl 24
Vor mittlerweile ca. 7 Jahren studierte ich
intensiv diverse Kugelpackungsschemen.
Schon damals kam ich zu dem Schluss, dass
die dichteste Kugelpackung mit dem so
genannten kubisch flächenzentrierten Gitter
jene Kugelpackung präsentiert, welche die
perfekteste Symmetrie besitzt.
Man nennt diese Variante auch die
Kepplersche Kugelpackung.
Am einfachsten kann man dieses Packungsschema
nachvollziehen, wenn man sich einen Apfelsinen-
stapel vorstellt, wie er früher in den Schaufenstern
der Obstläden zu sehen war.
Zuerst legt man eine quadratische Fläche mit
Apfelsinen voll und legt als zweite Schicht die
Apfelsinen in die jeweiligen Lücken der ersten
Schicht.
|
|
Die Bezeichnung Kepplersche Kugelpackung hat ihren Namen von der Tatsache, dass sich schon Keppler mit dieser Packungsvariante intensiv beschäftigte. Damals waren es allerdings noch nicht Apfelsinen sondern Kanonenkugeln.
Nun fand ich damals in Wissenschaft Online folgenden Artikel, der seit einiger Zeit leider schon wieder gelöscht ist:
Die Pyramidenzahlen sind:
P1 = 1
P2 = 1 + 4 = 5
P3 = 1 + 4 + 9 = 14
und so weiter.
Man könnte sie eine nach der anderen ausrechnen,
aber es gibt eine allgemeine Regel. Gerade so,
wie es eine einfache Formel für die n-te
Quadratzahl gibt..."
"Und zwar?" fragte Scheffle.
"Nun, n hoch 2. Wie der Name schon sagt.
Und die n-te Dreieckszahl ist n (n + 1) / 2
Schreiben wir das als
Qn = n hoch 2
Dn = n (n + 1) / 2.
Ich habe soeben ausgerechnet, daß die n-te Pyramidenzahl
Pn = n (n + 1) (2 n + 1) / 6
ist. Daraus kann man herleiten, daß
P24 = 24 x 25 x 49 / 6 = 4900 ist,
und das ist eine Quadratzahl.
|
|
Denn für n = 24 ist jede der Zahlen
n / 6, n + 1 und 2n + 1
eine Quadratzahl - ein sehr ungewöhnliches Zusammentreffen.
"Ah ja. Geht das auch für andere Quadratpackungen?"
"Nun, wir müssen das 1x 1-Paket nur umetikettieren. Es ist eine Pyramide der Höhe 1."
"Sehr witzig. Irgendwelche anderen Quadrate?"
"Ich kann keine finden", antwortete Lilli.
Der britische Mathematiker
George N. Watson (1886 bis 1965)
hat bewiesen,
daß P1 und P24
die einzigen Quadratzahlen unter den
Pyramidenzahlen sind.
Das war lange vermutet worden,
aber ein Beweis stand aus.....
Zitat Ende.
Vergleichen Sie bitte diesen Sachverhalt
mit dem nun Nachfolgenden!
|
|
|
 |
|
|
So verfährt man weiter, bis man als letzte Schicht
nur noch eine einzige Apfelsine obendrauf legen
kann.
Das Ergebnis ist eine perfekte Pyramide,
so wie man sie in Ägypten auf dem Gizeh-Plateau
bewundern kann.
|
|
 |
|
|
|
|
Eine interessante Besonderheit innerhalb der Quadratzahlen wird leider nicht für besonders wichtig erachtet, weshalb ich diese hier zeigen möchte:
Zählt man nämlich die kleinen Quadrate innerhalb der Kantenlängen der sich daraus ergebenen großen Quadrate so wie in der rechten Animation dargestellt, ringförmig von innen nach außen ab, so kommen wir immer auf ein Vielfaches von 8:
Kantenlänge 3 = 8 x 1
Kantenlänge 5 = 8 x 2
Kantenlänge 7 = 8 x 3
Kantenlänge 9 = 8 x 4
Kantenlänge 11 = 8 x 5
Kantenlänge 13 = 8 x 6 usw...
Logischerweise ergeben dann die entsprechenden Kantenlängen nur ungerade Zahlen!
Bitte nicht verwechseln mit dem
Aufkumulieren von ungeraden Zahlen,
welche wieder die Quadratzahlen ergeben!
|
|
 |
|
Quadratzahlen, Primzahlen und die Zahl 24
Eine Quadratzahl ist eine Zahl, die durch die Multiplikation einer ganzen Zahl mit sich selbst entsteht. Beispielsweise ist 25 = 5·5 eine Quadratzahl.
Die ersten Quadratzahlen sind:
1, 4, 9, 16, 25, 36, 49, 64, 81, 100, …
Die Bezeichnung "Quadratzahl" leitet sich von der geometrischen Figur des Quadrats her. Die Anzahl der Steine, die man zum Legen eines Quadrats benötigt, ist immer eine Quadratzahl.
So lässt sich beispielsweise ein Quadrat mit der Seitenlänge 5 mit Hilfe von 25 Steinen legen.
Aufgrund dieser Verwandtschaft mit einer geometrischen Figur zählen die Quadratzahlen zu den figurierten Zahlen, zu denen auch die Dreieckszahlen gehören.
Diese Begriffe waren schon den griechischen Mathematikern der Antike wie z.B. Pythagoras bekannt.
|
|
 |
|
|
Aus diesem Sachverhalt lässt sich nun folgende rechts abgebildete Grafik ableiten:
Wir zählen die kleinen Quadrate in den Seitenlängen der großen Quadrate so ab, das immer ein Vielfaches von 24 dabei herauskommt.
Die links untereinander geschriebenen roten Zahlen in der Grafik 1, 5, 7, 11, 13, 17, 19...
sind nun die Seitenlängen der Quadrate.
Es verschwinden dabei also alle dreiteilbaren ungeraden Zahlen.
Übrig bleibt die lückenlose Folge der Primzahlzwillingsplätze, der Sechsertakt
der Form 6n ± 1 inklusive aller
entsprechenden Pseudoprimzahlen.
Die rechts daneben stehenden Vielfachen von 24 sind die Anzahl der kleinen Quadrate innerhalb der entsprechenden, sich abwechselnden Bereiche.
Man muss auch hier wieder erkennen, dass die Primzahlen 2 und 3 in ganz besonderer Weise zu betrachten sind.
Es sind die einzigen Primzahlen, die sich nicht im Sechsertakt der Form 6n ± 1 befinden, und die nun auch nicht in dieser Geometrie zu finden sind. (Kantenlängen der Vierecke)
Wohl aber die Ziffer 1 !
Nichts worüber man sich wundern muss, aber man muss diese Tatsache anerkennen.
Den gleichen Sachverhalt könnte man auch mit einem Kreisraster, bzw. mit Kugeln darstellen.
Die Vielfachen von 24 aufkumuliert in den dunklen Quadraten zeigt die n-Folge, die aufkumuliert die Dreieckszahlen ergeben, in den hellen Quadraten dagegen die ungerade n-Folge 1, 3, 5, 7, 9... die aufkumuliert wieder die Quadratzahlen ergeben.
|
|
 |
|
 |
|
|
|
|
|
|
 |
|
Kusszahlen und die Zahl 24
Zu diesem Thema Wikipedia 10.01.2012:
In der Geometrie ist die n-te Kusszahl
(auch Kontaktzahl) die maximale Anzahl
an n-dimensionalen Einheitskugeln, also
Kugeln mit Radius 1, die gleichzeitig eine
weitere solche Einheitskugel im euklidischen
Raum berühren können, ohne dass
Überschneidungen auftreten.
Zusätzliche Bedingung: die Mittelpunkte der Kugeln müssen in einem Gitter liegen.
(Gitterkusszahlen).
Als Kusszahlenproblem ist das Fehlen einer allgemeinen Formel zur Berechnung der Kusszahlen bekannt.
Hier von mir eine wissenschaftlich nicht korrekte, aber vielleicht allgemeinverständlichere Erklärung:
Kusszahl = Die maximal mögliche Anzahl
von gleich großen "Umkugeln", die eine
"Zentralkugel" berühren können.
Für jede Dimension gibt es eine
eigene Kusszahl.
In der ersten Dimension (Linie) ist die Einheitskugel eine Strecke, an deren Endpunkten jeweils eine weitere Strecke hinzugefügt werden kann.
|
|
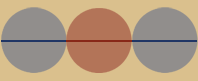
Die Kusszahl für Dimension 2 ist folglich 6.
Der Zentralkreis in der Mitte ist rotbraun dargestellt, die 6 Umkreise graublau.
In der dritten Dimension (Raum) haben wir auch einen dreidimensionalen Körper, also eine Kugel.
|
|
12 gleich große Kugeln passen genau um
eine 13. Kugel, siehe die zwei Abbildungen oben rechs. Beide Bilder zeigen die selbe Struktur, es handelt sich lediglich um zwei verschiedene Symmetrieansichten.
Die Kusszahl für Dimension 3 ist folglich 12.
|
|
|
 |
 |
|
|
 |
|
|
 |
|
|
Die Kusszahl für Dimension 1 ist folglich 2.
In der zweiten Dimension (Fläche) ist die
Einheitskugel ein Kreis. 6 gleichgroße Kreise
passen genau um einen 7. Kreis!
siehe die Abbildung oben links.
|
|
|
|
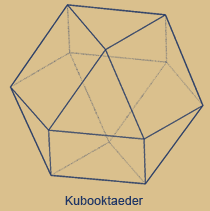
Dies entspricht einem Ausschnitt der Kepplerschen
Kugelpackung, es handelt sich dabei wieder um
das so genannte kubisch flächenzentrierte Gitter.
Verbindet man die Mittelpunkte der Kugeln, dann ergeben die Außenkonturen ein Kubooktaeder.
|
|
Das Kubooktaeder setzt sich aus 4 ineinander verschränkten 6-Ecken zusammen. 4 x 6 = 24.
Siehe Abbildung in der Mitte.
Oder anders betrachtet:
Das Kubooktaeder hat 24 Kanten.
|
|
 |
|
Wie sieht es nun mit den theoretisch möglichen Dimensionen oberhalb unserer 3. Dimension aus?
Dazu Wikipedia weiter:
Erst Anfang des 21. Jahrhunderts wurde
bewiesen, dass die Kusszahl für die vierte
Dimension die Zahl 24 ist.
Florian Pfender, Günter M. Ziegler
Ferner sind die Kusszahlen für die Dimensionen
n = 8 (240) und n = 24 (196.560) bekannt;
im 24-dimensionalen Raum werden die Kugeln
auf den Punkten des Leech-Gitters platziert,
sodass kein Platz übrig ist.
|
|
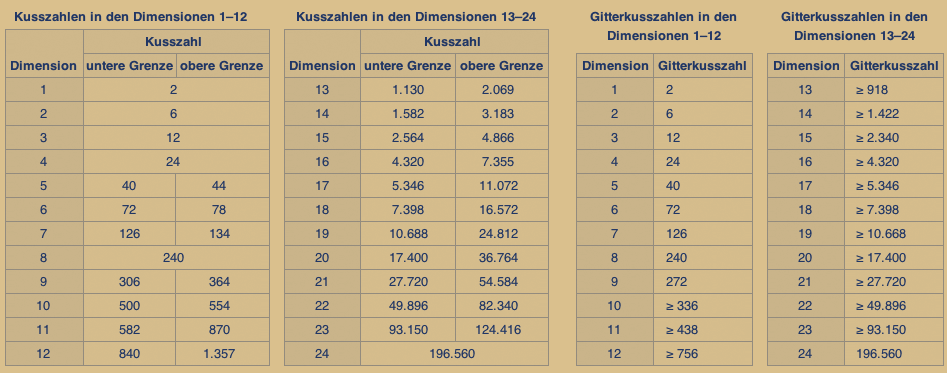
Die folgende Tabelle gibt die bekannten Grenzen
für die Kusszahl bis zur Dimension 24 wieder.
Wikipedia Ende.
Unten sehen Sie die entsprechenden Tabellen,
die auch in Wikipedia zu finden sind.
Zu sehen sind die absoluten Werte, die im Zusammenhang mit der Ziffer 24 errechnet wurden, wärend alle anderen Werte Von-Bis-Werte sind.
In diesem Zusammenhang ist also das
Leech-Gitter interessant. |
|
Unabhängig von der Tatsache, dass mit dem Beweis der Kusszahl 24 der vierten Dimension vermutlich auch die entsprechenden Vielfachen von 24 korrekt ermittelt werden konnten.
Denn:
Fakt ist die Tatsache, dass die Ziffer 24 in den
Fraktalen von Kugelpackungen innerhalb
des dreidimensionalen Raumes aus
kombinatorischen Gründen eine wichtige
Rolle spielen muss.
|
|
 |
|
 |
|
|
|
 |
|
|
Obige Anmerkung von der Bedeutung dier Ziffer 24 in den Fraktalen von Kugelpackungen innerhalb des dreidimensionalen Raumes möchte ich im folgenden kurz erläutern:
Die Flächen der Kristallgitter von Kugelpackungen setzen sich ausschließlich
aus Dreiecken, Quadraten bzw. auch
Sechsecken ( 6 Dreiecke ) zusammen.
Das wiederum hängt mit der Tatsache zusammen, dass eben nur genau diese drei Polygone in der Ebene mit sich selbst allein oder im Raum miteinander kombiniert, lückenlos pflasterbar sind.
Hier zuerst mal die wichtigsten Symmetrien, die in den Kristallgittern von Kugelpackungen vorkommen:
Hexaeder: 6 x 4-Ecke = 24
Oktaeder: 8 x 3-Ecke = 24
Sterntetraeder: 24 x 3-Ecke
Kubooktaeder: 3 x 8, oder 4 x 6 = 24
Tetraeder: 4 x 3-Ecke = 24 / 2
Nun muss man sich vor Augen halten, dass es sich bei Kristallgittern von Kugelpackungen tatsächlich um echte Fraktale handelt.
Genau genommen handelt es sich unter anderem auch um dreidimensionale Sierpinski-Dreiecke, also Sierpinski-Tetraeder und
-Oktaeder.
Da nun die Anzahl der Fraktale der jeweiligen Iterationsstufe eines n-Ecks identisch mit seinen Ecken ist, haben diese Symmetrien in der ersten Iterationsstufe ebenfalls immer entsprechende "fraktale Flächen".
|
|
Konsequenterweise sieht das so aus:
Oktaeder: 3 x 8 = 24 Flächen gesamt
Hexaeder: 4 x 6 = 24 Flächen gesamt
Kubooktaeder: 3 x 8, und 4 x 6 = 2 x 24 (48)
Sterntetraeder: 3 x 24 Flächen gesamt (72)
Tetraeder: 3 x 4 = 12 Flächen gesamt, also 24 / 2
|
|
|
Der dreidimensionale Raum lässt sich nur mit drei der fünf platonischen Körper lückenlos füllen: mit Oktaeder und Tetraeder im Verbund, oder mit Hexaedern (Würfeln) allein.
Sterntetraeder und Kubooktaeder sind lediglich aus diesen drei Körpern zusammengesetzt.
Wenn also diese "Geometrie der lückenlosen
Raumfüllung" in mehrfacher Weise mit der
Ziffer 24 korreliert, könnte es dann sein,
dass diese hoch zusammengesetzte Zahl
nicht nur bei der Primzahlverteilung eine
wichtige Rolle spielt, sondern auch
unmittelbar mit dem Raum selbst tun hat?
Interessanterweise spielt die Zahl 24 im Zusammenhang mit einem 4-dimensionalen Raum auch in Peter Plichtas Überlegungen
die tragende Rolle.
Was aber noch viel bemerkenswerter ist:
Kusszahlen und Kristallgitter von Kugelpackungen werden von Plichta überhaupt nicht erwähnt, andererseits spielt das Sierpinskidreieck in seinen Ausarbeitungen eine wichtige Rolle.
Plichtas Theorien gibt es schon weit über 20 Jahre. Aber erst 2006 wurde die Kusszahl 24 in der theoretisch 4. Dimension mathematisch bewiesen! In wieweit also auch hier ein
direkter Zusammenhang besteht, sollte
untersucht werden.
Siehe dazu auch:
DIE GEOMETRIE DER LÜCKENLOSEN RAUMFÜLLUNG
|
|
|
 |
|
Die Abbildung zeigt ein Fraktal des Oktaeders
in der ersten Iterationsstufe. Jede Dreiecksfläche teilt sich – genau wie beim Sierpinski-Dreieck – in drei kleine Dreiecke auf. Dabei entstehen 24 Oktaederflächen. Schneidet man die Spitzen weg, haben wir wieder ein Kubooktaeder.
|
|
 |
|
|
Fibonaccizahlen und die Zahl 24
Der Fibonacci-Folge wird allgemein eine größere Aufmerksamkeit zuteil, da sie in der Natur (zB. Blattstellungen) viele Korrelate hat, zum anderen auch mit dem Goldenen Schnitt im Zusammenhang steht, mit dem sie jedoch nicht identisch ist.
Auch im Pascalschen Dreieck findet sich die Fibonacci-Folge. Deshalb hier ein interessanter, kaum bekannter Sachverhalt, der mit der Ziffer 24 zu tun hat:
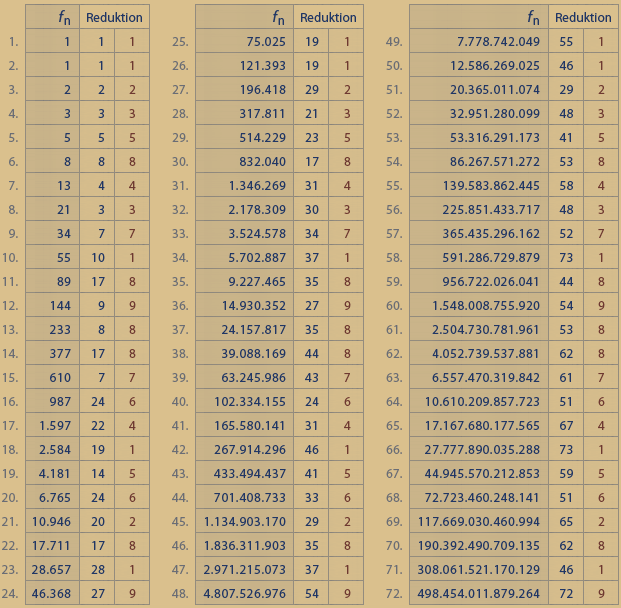
Reduziert man nämlich die Fibonacci-Folge
auf einstellige Quersummen so wie rechts dargestellt, dann wiederholen sich diese bis unendlich immer in 24er Intervallen.
Nun muss man sich natürlich darüber im Klaren sein, dass Quersummen immer vom jeweiligen Zählsystem abhängig sind, in unserem Fall also natürlich vom Dezimalsystem.
Da aber diese Internetseite die Dezimalcodierung
der Simplexe, und die damit verknüpfte Primzahlverteilung im Zusammenhang mit der Ziffer 24 zum Thema hat, möchte ich eben auf diese bemerkenserwerte Tatsache hier an dieser Stelle unbedingt aufmerksam machen.
Dazu ein interessantes Detail mit Blick auf unser Dezimalsystem:
Stellt man nämlich von einem dieser 24er Intervalle die ersten 12 Quersummen den zweiten 12 Quersummen gegenüber, so ergänzen sie sich immer zur Ziffer 9:
|
|
 |
|
|
erste 12: 1 1 2 3 5 8 4 3 7 1 8 9
zweite 12: 8 8 7 6 4 1 5 6 2 8 1 9
Quersumme: 9 9 9 9 9 9 9 9 9 9 9 9
|
|
|
Die Differenz einer Zahl im Dezimalsystem und
ihrer Quersumme ist immer durch 9 teilbar
(Stichwort Neunerprobe).
Hier zwei Links zum Thema Fibonaccizahlen
und die Ziffer 24 (keine Matheseiten!!!):
Joseph Turbeville
Jain Mathemagics
|
|
 |
|
|
|
|
Weitere wichtige Themen zur Ziffer 24 wären:
• Das Leech-Gitter in "Dimension" 24
• Dreieckszahlen Dezimalcodierung
und die Zahl 24 (Peter Plichta)
• Dezimalcodierung, Primzahlen
und die Zahl 24 (Peter Plichta)
|
|
Vielen Dank den Lesern, die mich auf
einige der hier dargestellten
Zusammenhänge hingewiesen haben.
Gern nehme ich weitere korrigierende
Hinweise und auch Kritiken entgegen.
Meine Adresse ist:
mail-at-holger-ullmann-dot-de
^ Zurück nach oben ^
|
|
Mit Blick auf die Primzahlproblematik
in Verbindung mit der Zahl 24 und der
Dezimalcodierung der Primzahlverteilung,
die in der Geometrie der Simplexe zu
finden ist, möchte ich noch einmal auf die
Pythagoreische Tetraktys der Form:
1 + 2 + 3 + 4 = 10 hinweisen, um ihr
1 x 2 x 3 x 4 = 24 gegenüber zu stellen.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|