|
|
|
|
|
|
|
|
|
|
Das determinierende System, welches die Primzahlen als Zwillingspaare ordnet, resultiert aus der Dreiteilung der Zahlen und ihrer spiegelsymmetrischen Anordnung, nämlich aus dem 6er Takt nach Leibnitz.
Das Verständnis um diese Tatsache ist die Vorraussetzung um die nun hier gezeigten Zusammenhänge zu begreifen.
Deshalb lesen Sie dazu bitte zuerst:
TETRAKTYS PART 1 – DIE ORDNUNG
DER PRIMZAHLEN
|
Ab der Ziffer 25 wird ja nun diese strenge, spiegelsymmetrische Ordnung aus kombinatorischen Gründen wieder zerhackstückt, denn die 25, die sich auf einem potentiellen Primzahlzwillingsplatz befindet, ist ohne Rest
durch die Ziffer 5 teilbar.
Und genau hier beginnt die scheinbar unregelmäßige Primzahlverteilung, welche den Mathematikern so viel Kopfzerbrechen bereitet.
Es gibt dazu mindestens zwei grundsätzliche Überlegungen.
Die Mehrzahl der Mathematiker vermutet, dass die Primzahlen aus sich selbst heraus geordnet sind, da sich ja alle Zahlen aus Primfaktoren zusammensetzen. Mit hinreichend großen |
Zahlenmengen kann man dann unter Zuhilfenahme
des Computers auch durchaus entsprechende Grafiken erstellen, in denen eine unregelmäßige Regelmäßgikeit erkennbar ist.
Die Riemannsche Zetafunktion ist ein weiterer
Weg. Hier wird mit Hilfe einer "topologischen Landschaft" erkannt, dass alle Primzahlen auf
einer Geraden durch den Punkt 1/2 auf dem
Realteil liegen.
Kann man deshalb behaupten, dass die Zahl 2,
als inverse von 1/2, eine große, vielleicht sogar entscheidende Bedeutung für das Primzahlverständniss hat?
Schauen wir uns folgende Tabelle an:
|
|
 |
|
|
 |
|
|
|
|
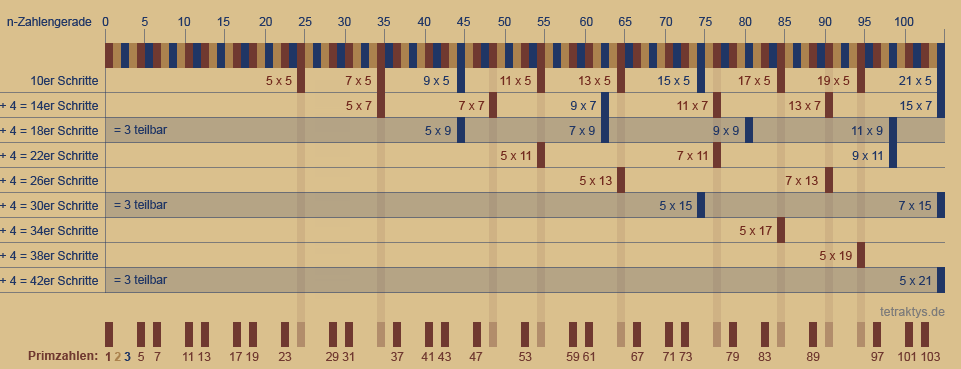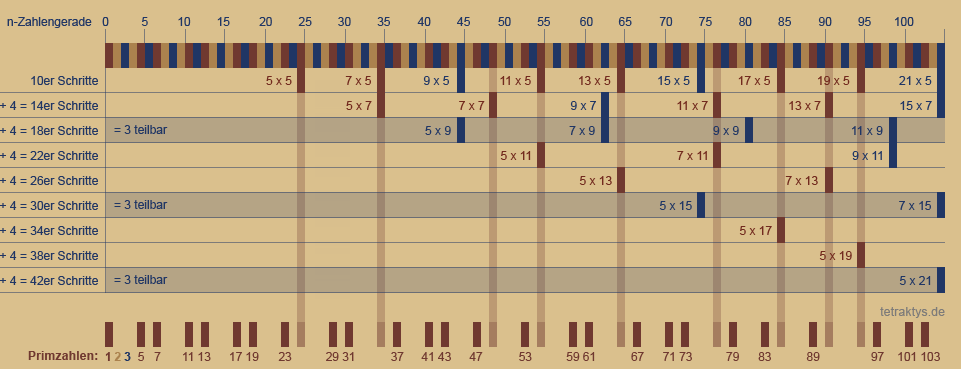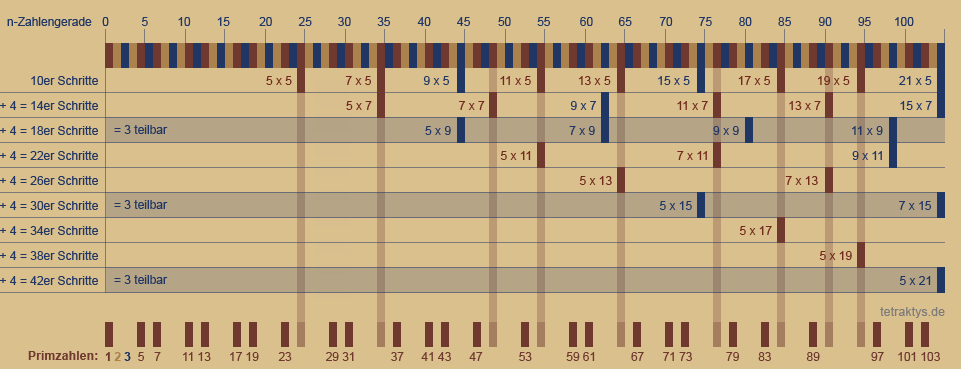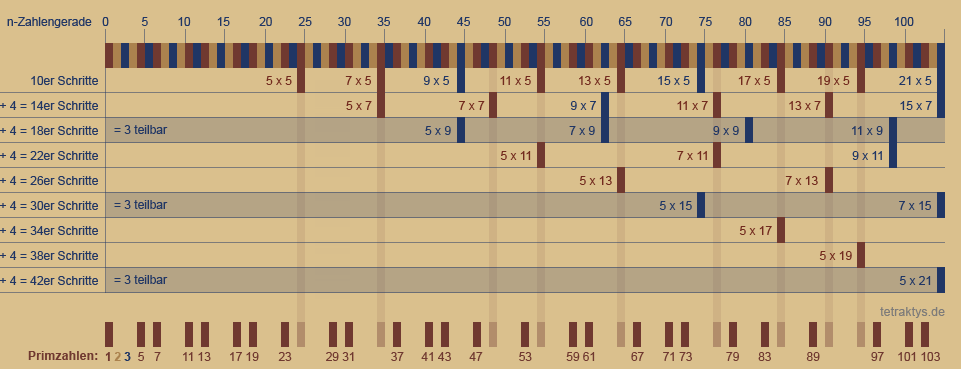
Ganz oben sehen wir die Zahlengerade mit der spiegelsymmetrischen Ordnung des 6er Taktes nach Leibnitz der Form 6n ± 1 wie bereits beschrieben in:
TETRAKTYS PART 1 – DIE ORDNUNG
DER PRIMZAHLEN
|
|
Und jedes folgende Raster ist um jeweils
4 Ziffern weiter, also:
10er Schritte ab 25 = 5 x 5
14er Schritte ab 35 = 5 x 7
18er Schritte ab 45 = 5 x 9
22er Schritte ab 55 = 5 x 11
26er Schritte ab 65 = 5 x 13
30er Schritte ab 75 = 5 x 15
34er Schritte ab 85 = 5 x 17
38er Schritte ab 95 = 5 x 19 u.s.w...
Um die Ordnung des Systems zu verstehen, sind alle ungeraden Zahlen zu betrachten, also auch dreiteilbare Zahlen außerhalb der potenziellen Primzahlzwillingsplätze.
Diese sind blau markiert.
4er Abfolge: 10, 14, 18, 22, 26, 30, 34, 38...
10er Folge: 25, 35, 45, 55, 65, 75, 85, 95...
Im unteren Bereich der oberen Tabelle sehen wir nun das Destillat des Systems, die lückenlose Folge der Primzahlen.
Diese Ordnung zeigen auch die
Sternpolygone der Simplexe, wenn
man diese im Lambdoma auffächert.
|
|
Über die Zahl 1 und die Primzahlen 2 und 3 wurde im vorangegangenen Thema bereits geschrieben.
Die Primzahlverteilung ist also weiterhin unregelmäßig. Aber es gibt eine strenge Ordnung, welche die Primzahlen auf ihre Plätze verweist.
Im Groben haben wir hiermit das "Mysterium" der Primzahlverteilung entschleiert.
Mit Erkenntnis dieses Sachverhaltes könnte man sich eigentlich schon begnügen. Wenn dieses System nicht viel zu schön wäre, um weiter untersucht zu werde.
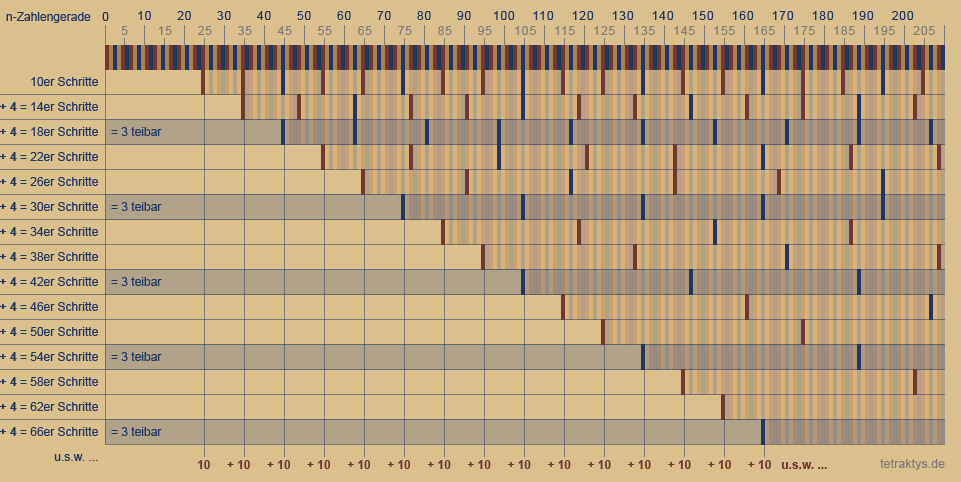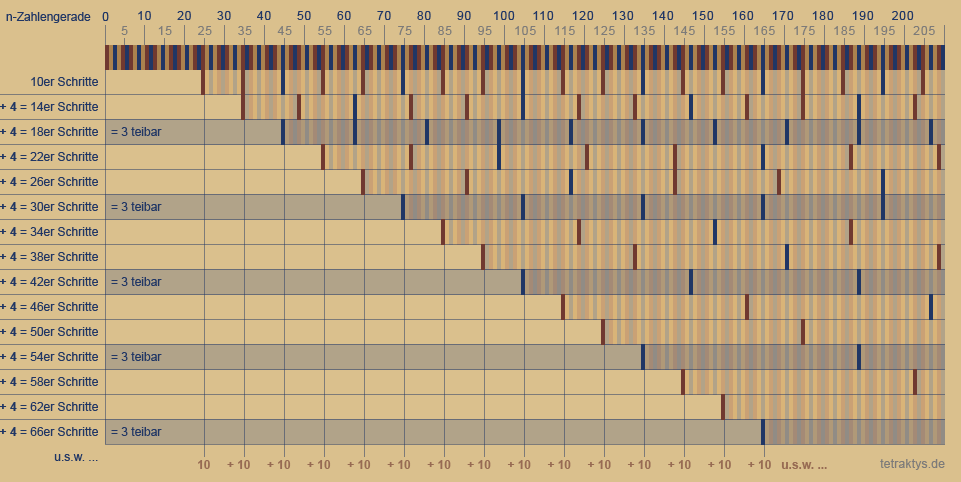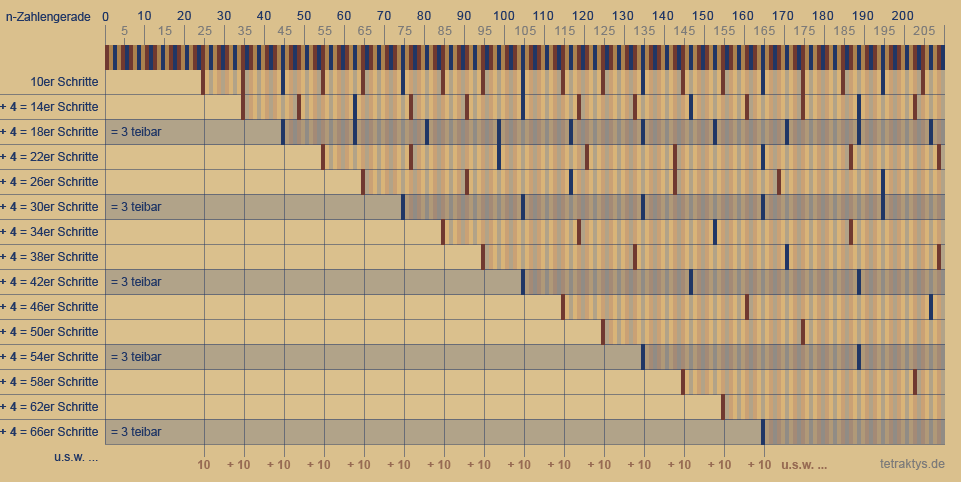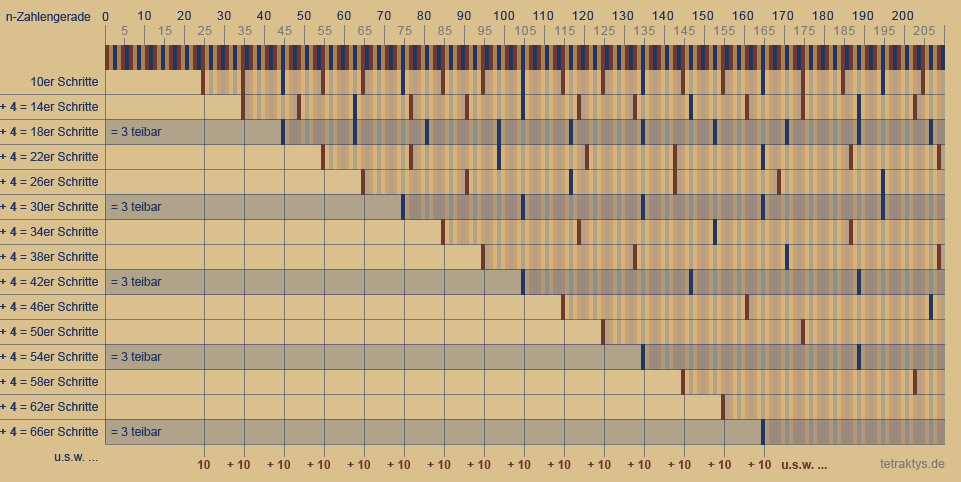
Die folgende Tabelle zeigt den gleichen Sachverhalt noch einmal eindrucksvoll mit einer größeren Zahlenmenge.
Man beachte die 4er-Schritte der Vertikalen und die 10er-Schritte in der Horizontalen.
Was könnte das mit der pythagoreischen
Tetraktys 1+2+3+4=10 zu tun haben?
Eine Frage, die kein Berufsmathematiker
ernsthaft diskutiert haben möchte...
Die Viererschritte entstehen dadurch, dass durch die Eigenschaft gerader und ungerader Zahlen im Kooridnatensystem ein Doppelungseffekt entsteht, dazu später noch einmal mehr.
Deutlich interessanter sind die 10er Schritte. |
|
 |
|
|
|
|
Die linke Spalte zeigt die Schrittfolge sich überlagernder Raster, welche absolut alle Nichtprimzahlen der Form 6n ± 1 aussieben.
Und natürlich handelt es sich hierbei auch um das altbekannte Sieb des Eratosthenes.
Allerdings aus einen völlig anderen Blickwinkel heraus, wie man nun dieser Tabelle entnehmen
kann:
Denn dem System der Primzahlverteilung
liegt eine Dezimalcodierung zu Grunde.
Jedes nachfolgende Raster startet bis unendlich immer um 10 versetzt!
|
|
 |
|
|
 |
|
|
|
In diesem Zusammenhang kommen wir zur eingangs gestellten Frage, was dieses System mit der Riemannschen Zetafunktion und den so genannten Nullstellen auf der Geraden = 1 / 2 auf dem Realteil zu tun haben könnte. Dazu denken wir das System unterhalb der Ziffer 25 weiter und stoßen auf die Ziffer 5, dessen Raster in 2er Schritten alle ungeraden Zahlen bis abzählbar unendlich trifft:
|
|
 |
|
|
Hier also noch einmal die Abfolge beginnend
bei der 5:
|
|
|
Warum erwähne ich diese simple Tatsache?
Nun, es lohnt sich darüber nachzudenken, ob der Ziffer 5 – natürlich im Zusammenspiel mit der Zahl 2 – grundsätzlich eine Schlüsselrolle bei Zahlenbrüchen zukommt – und das unabhängig von unserem Dezimalsystem!
Denn nimmt man noch alle geraden Zahlen
hinzu, dann sehen wir, um was es wirklich
geht! Alle 5er-Sprünge werden mit allen
geraden Zahlen (2) dividiert:
5 x 1 = 5 / 2 ...also 2,5 x 10 = 25
5 x 2 = 10 / 4 ...also 2,5 x 10 = 25
5 x 3 = 15 / 6 ...also 2,5 x 10 = 25
5 x 4 = 20 / 8 ...also 2,5 x 10 = 25
5 x 5 = 25 / 10 ...also 2,5 x 10 = 25
5 x 6 = 30 / 12 ...also 2,5 x 10 = 25
5 x 7 = 35 / 14 ...also 2,5 x 10 = 25
5 x 8 = 40 / 16 ...also 2,5 x 10 = 25
5 x 9 = 45 / 18 ...also 2,5 x 10 = 25 u.s.w...
|
|
|
Eine weitere interessante Frage:
Was hat diese Dezimalkodierung mit der zweiten und vierten geometrischen Startfigur der Tetraktys, dem Pentagramm ( 5/2 = 2,5 ) und dem doppelten Pentagramm ( 10/4 = 2,5 ) zu tun?
Siehe dazu:
Der Schlüssel zur Tetraktys
Denn die mathematische Kernaussage
eines Pentagramms ist klar:
5 geteilt durch 2 = 2,5! Wikipedia
Jeder zweite Punkt eines 5-Ecks wird verbunden, 2,5 x 10 = 25.....
...und hier bei Ziffer 25 beginnt die scheinbar chaotische Primzahlverteilung...
Wie korelliert die Symmetrie der Simplexfiguren, welche sich aus Sternpolygonen wie dem Pentagramm zusammensetzen, mit dem hier beschriebenen Sachverhalt?
Mit Klärung dieser Frage bekommen wir ein tieferes Verständnis für die Zusammenhänge zwischen der pythagoreischen Tetraktys und dem Erkennungs-
zeichen des antiken pythagoreischen Bundes,
dem Pentagramm, denn:
2,5 = Zwei und ein Halbes entspricht: 1 zu 4 |
|
|
|
|
2er Schritte ab 5 = 5 x 1
6er Schritte ab 15 = 5 x 3
10er Schritte ab 25 = 5 x 5
14er Schritte ab 35 = 5 x 7
18er Schritte ab 45 = 5 x 9
22er Schritte ab 55 = 5 x 11
26er Schritte ab 65 = 5 x 13
u.s.w...
|
|
|
|
Konsequenterweise müsste man ja jetzt folgende dumm-ketzerische Frage stellen:
Warum siebt das Raster ab der Ziffer 5, welches alle Primzahlen und natürlich auch alle ungeraden Zahlen beinhaltet (also zur Hälfte auch alle dreiteilbaren Zahlen außerhalb des Zwillingsrasters), keine Primzahlen aus?
Denn:
wenn es das täte, hätte es Primzahlen nie
gegeben – außer den "Primzahlen" 1, 2 und 3...
Die Antwort auf diese Frage gibt die Ziffer 1 innerhalb obiger Abfolge, also:
2er Schritte ab 5 = 5 x 1
Worin könnte nun ein Zusammenhang
bestehen zwischen der 1/2 und der inversen
2 bezüglich der Riemannschen Zetafunktion? Der Hinweis den ich dazu gebe, ist vielleicht so simpel, dass er auf einen Berufsmathematiker beleidigend wirkt. Ich schreibe ihn trotzdem
hier her:
>>> 2er Schritte ab 5
>>> 1 / 2 also 0,5 x 10 = 5
Warum ich zu 1 / 2 noch 0,5 geschrieben
habe:
1 / 2 ...also 0,5 x 10 = 5 ...also 5 x 1
3 / 2 ...also 1,5 x 10 = 15 ...also 5 x 3
5 / 2 ...also 2,5 x 10 = 25 ...also 5 x 5
7 / 2 ...also 3,5 x 10 = 35 ...also 5 x 7
9 / 2 ...also 4,5 x 10 = 45 ...also 5 x 9 u.s.w...
|
|
 |
|
|
|
 |
|
Diese Dezimalcodierung ist keine Täuschung des im Dezimalsystem rechnenden menschlichen Geistes, denn sie ist in der Geometrie der Simplexe enthalten.
Die Simplexe sind die exakte geometrische
Darstellung natürlicher Zahlen. Und Geometrie
"denkt" und "rechnet" nicht in irgendeinem
Zählsystem... Sehen Sie hier:
SIMPLEX – DER FESTE
AGGREGATZUSTAND DER ZAHL
|
|
| Das Zusammenspiel von ungeraden und geraden Zahlen ergibt – genau wie beim 6er-Takt nach Leibnitz vom Dreieck zum Hexagramm – die Doppelung des Pentagramms zur heiligen Zahl 10 der Pythagoreer. 2,5 x 4 ist 10. |
|
|
 |
|
|
 |
|
Am 26. November 2010 stieß ich bei googeln nach dem Stichwort "Tetraktys" auf eine Buchbesprechung über den Roman "Against the Day" des amerikanischen Schriftstellers Thomas Ruggles Pynchon.
Zitat Überschrift: "Im Universum von «Against the Day» melden sich die Dinge, die es gibt, zuerst in der Mathematik. Nur die Mathematiker merken es nicht."
In dieser Buchbesprechung vom bekannten Literaturwissenschaftler und Professor für Ästhetik
|
|
und Geschichte der Medien in Berlin Prof. Dr. Friedrich Kittler im März 2007 kommt all das zur Sprache, was zum Thema Mathematik in Verbindung mit der Tetraktys und er Primzahl-
verteilung auch von meiner Seite zu sagen wäre. Besonders interessant dabei ist die gedankliche Verbindung zwischen der Tetraktys und der Riemanschen Zetafunktion. Ob Herrn Kittler ein direkter Zusammenhang bewusst ist, geht aber
aus diesem Artikel nicht hervor.
Hier nun der Link zum Artikel.
|
|
Thomas Ruggles Pynchon studierte zuerst Physik und danach Literatur. Nach seiner beruflichen Laufbahn als technischer Redakteur bei Boig schottete er sich 1963 von der Öffentlichkeit ab, um sich seiner schriftstellerischen Laufbahn zu widmen. Seine Romane sind nicht einfach zu lesen und fordern vom Leser einiges an geistiger Manöverierfähigkeit.
Bitte lesen Sie weiter unter:
DIVISIONSTABELLE & SIEB DES ERATOSTHENES
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|