|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
|
Der amerikanische Ingenieur und Visionär
Richard Buckmister Fuller (1895-1983)
veröffentlichte 1975 mit „Synergetics“ eine
Kosmologie und Entwurfstheorie.
|
|
 |
|
 |
|
|
|
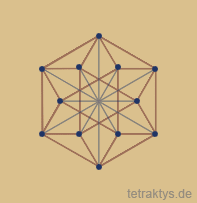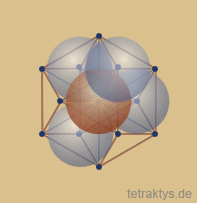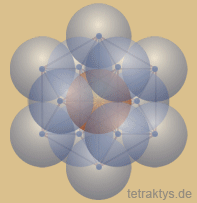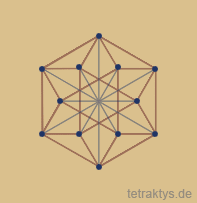
Buckminster Fullers Isotropic Vector Matrix
ist >das< Raumgitter, dessen hohe Symmetrie
durch dichtest gepackte Kugeln begründet ist.
Exakt die selbe Struktur weckte schon
400 Jahre früher das Interesse des
Mathematikers, Astronom und Mystikers
Johannes Kepler (1571-1630)
Das wird verständlich, wenn man sowohl den
kosmologisch philosophischen Backround
Kepplers, als auch diese interessante Struktur
selbst kennt und für sich verstanden hat.
Das Studium der sechszähligen Symmetrie von
Schneeflocken führte Kepler zu Berechnungen
der maximalen Dichte von Kreisanordnungen
und Kugelpackungen.
Nach ihm wurde diese Matrix auch
"Keplersche Kugelpackung" benannt.
Die korrekte Bezeichnung des Kristallgitters
dieser dichtesten Kugelpackung ist:
Kubisch flächenzentriertes Gitter.
|
|
Abb. links: Das Kubooktaeder ummantelt mit einer Schicht der Buckminster Isotropic Vector Matrix, zeigt die "geometrische Verwandtschaft" mit diesem Körper.
Abb. rechts: Das Kubooktaeder ist der Koordinationspolyeder der kubisch dichtesten Kugelpackung. Jede Kugel (Atom) ist von 12 gleichartigen Kugeln umgeben, welche alle die zentrale Kugel berühren.
|
|
Die „Geometrie des Denkens“, so der Untertitel,
verweist bereits auf Fullers ontologische Differenz
zwischen einer Kosmologie (synergy), und einer
Geometrie als entsprechender praktischer
Erkenntnistheorie.
Grundlage der Theorie ist die Annahme,
das Tetraeder und seine Beziehung zur
Sphäre (Kugel) liefere die mathematische
Vorlage für das Universum.
|
|
|
 |
|
|
|
 |
|
 |
|
|
|
Das Studium geometrischer Gesetzmäßigkeiten war Johannes Kepler so wichtig, dass er sich mit einem Zirkel in der Hand portraitieren ließ. |
|
Die R. Buckminster Fullers isotropic Vektor Matrix
|
|
 |
|
|
|
Die Struktur vieler Metalle entspricht einer dichtesten Kugelpackung.
Die Anordnung von Atomen in einer dichtesten Kugelpackung entspricht einem wichtigen Grundprinzip bei der Bildung von Kristallen:
dem Prinzip der Minimierung des Volumens.
Das ist ein interessanter Denkansatz,
denn im Umkehrschluss könnte man auch
sagen:
Die Materie folgt der "Anatomie das Raumes"!
Denn:
Raum und Energie, bzw. Energie im Raum
und die Form einer Kugel stehen in einem
direkten Verhältnis zueinander, da sich
Energiequellen wie z.B. Licht, Wärme,- und
Schall gleichmäßig, also kugelförmig im
Raum ausbreiten, wenn sie von einer
zweiten Kraft nicht abgelenkt werden.
|
|
Die Kugel ist ohnehin das Grundprinzip der
Natur. Der "Mikrokosmos" der Atome und der
"Makrokosmos" (Sterne und Galaxien) haben
Kugelform und/oder bewegen sich in Kugel-
und Kreisbahnen.
So betrachtet könnte diese Matrix eine viel
größere Bedeutung haben, als man ihr bisher
zugestand. Ähnliche Überlegungen dazu gibt
es also seit Buckminster Fuller schon länger.
Aller Wahrscheinlichkeit nach hat diese Struktur
auch für den bis heute unverständlichen
Schöpfungsbericht des Sefer Jezira, dem ältesten
Buch der Kabbala gemäß platonischem
Gedankengut Pate gestanden.
Die folgenden Überlegungen gehen auch
genau in diese Richtung:
|
|
Es soll zum Nachdenken angeregt werden,
was diese Matrix so besonders macht und
wo es Schnittstellen zur Pythagoreischen
Tetraktys gibt.
Oder auf den Punkt gebracht:
Symmetrien, ihre Volumenverhältnisse, Raumwinkelsummen, und deren Korrellation
zu Gesetzmäßigkeiten in der Zahlentheorie – (z.B. Kreiszahl Pi und der Zusammenhang zur Riemanschen Zetafunktion) als Brücke zum Verständnis physikalischer Vorgänge.
Die nun folgenden Erläuterungen sollen erst
einmal helfen, sich ein wenig in die "Anatomie" dieser interessanten "Raummatrix"
reinzudenken.
|
|
 |
|
|
|
DIE "ANATOMIE" DER RAUMMATRIX – DIE DICHTESTE KUGELPACKUNG UND IHR KRISTALLGITTER
|
|
 |
|
|
|
|
|
|
|
|
 |
|
Ob man den Raum mit Würfeln vollstapelt
oder mit regelmäßigen Körpern, deren
Grenzflächen Dreiecke sind – bei scharfem
Hinsehen läuft das auf dasselbe hinaus.
Tetraeder-Oktaeder-Packungen, bzw.
Sierpinski-Tetraeder und Oktaeder sind
die dreidimensionale Entsprechung der
Eigenschaften von Dreieck und Quadrat,
der Pflasterbarkeit in der Ebene, siehe:
KREIS, DREIECK & QUADRAT
Wenn man auf jede Seitenfläche eines Oktaeders
ein Tetraeder gleicher Kantenlänge aufsetzt –
Seitenfläche auf Seitenfläche –, die freien
Tetraederflächen wieder mit Oktaedern bedeckt
und so weiter, dann füllt man auf die Dauer den
ganzen Raum lückenlos mit diesen Körpern.
An jeder Seitenfläche eines Körpers sitzt ein
Körper der jeweils anderen Sorte mit ebenfalls
genau einer Seitenfläche...
Christoph Pöppe http://spektrum.de
Die beiden Animationen rechts oben zeigen
diese "lückenlose Raumfüllung" in zwei
verschiedenen Ansichten.
Die roten Fragmente sind Tetraeder,
die blauen Fragmente sind Oktaeder.
Tetraeder (4-Flächner) und Oktaeder (8-Flächner)
sind zwei der fünf platonischen Körper.
Links zu sehen ein Tetraeder, also eine Pyramide
mit dreieckigem Grundriss und rechts ein halbes
Oktaeder, eine Pyramide mit quadratischem
Grundriss in der Draufsicht.
|
|
 |
|
 |
|
|
 |
|
|
|
Wir stapeln Ecke auf
Ecke Tetraeder (rot)
übereinander.
Dabei entstehen Oktaeder-Lücken (blau).
Das Ergebnis ist ein
Tetraeder-Fraktal.
|
Wir stapeln Ecke auf
Ecke Oktaeder (blau)
übereinander.
Dabei entstehen Tetraeder-Lücken (rot).
Das Ergebnis ist ein
Oktaeder-Fraktal.
|
|
|
|
Tetraeder |
|
|
Oktaeder |
|
|
Beide Pyramiden sind Teil ein und der selben Struktur – in einer jeweils anderen Seitenansicht!
|
|
 |
|
|
|
Eine kleine Änderung macht aus diesen winkelig, eckigen Strukturen etwas ganz anderes: Kugelpackungen!
Man blase in Gedanken jeden der Eckpunkte
der geometrischen Körper zu einer Kugel
auf, und zwar so groß, dass alle Kugeln
aneinander stoßen.
Dann hat man die berühmte Keplersche
Kugelpackung: die dichtestmögliche Packung
von Kugeln im Raum.
Unter allen Kugelpackungen die Schönste,
nämlich die mit der bestmöglichen
Symmetrie!
Schon Johannes Kepler (1571 - 1630) hatte
vermutet, dass es nicht möglich sei, den Raum
"sparsamer" mit Kugeln aufzufüllen als auf diese
Art, die jeder Obsthändler beim Orangenauftürmen
praktiziert. Aber erst 1998 gelang es Thomas
Hales, das auch mathematisch zu beweisen.
|
|
 |
|
|
|
|
Die obere Abbildung soll die Beziehung zwischen
dichtest gepackten Kugeln und dem daraus
resultierenden Kristallgitter zeigen.
Zwei Kugelschichten genügen, um den steten Wechsel der entsprechenden Tetraeder- und Oktaderlücken zu veranschaulichen.
Die Ecken der Kristallkörper sind ausnahmslos in den Mittelpunkten der Kugeln verortet!
|
|
Gleich große Kugeln erzeugen immer
auch gleiche Abstände und damit auch
regelmäßige Kristallkörper, bzw. platonische
Körper mit gleichen Ecken, Kanten und
Flächen.
Diese Abbildug zeigt lediglich die Ansicht der
Parkettierung mit Dreiecken bzw. Sechsecken.
Um die quadratische Parkettierung zu sehen,
muss diese Struktur um 60 Grad gedreht werden.
|
|
 |
|
 |
|
|
|
|
|
|
 |
|
 |
|
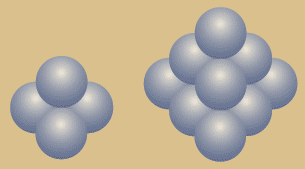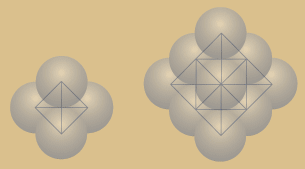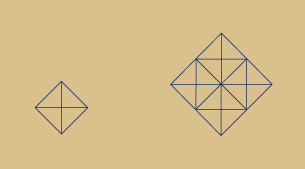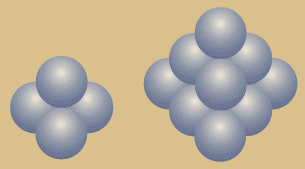
Die rechts abgebildeten Animationen zeigen die
dreieckige bzw. sechseckige und die
quadratische, um 60 Grad gedrehte Ansicht
ein und der selben Struktur am Beispiel des
Tetraeders.
Links immer jeweils als einfache
Figur, rechts als Fraktal. |
|
Diese Animation zeigt links ein einfaches Tetraeder, Im Wechsel als Kugelpackung und als Kristallgitter. Rechts daneben das Fraktal im ersten Rekursionsschritt. Hier die Ecken-Ansicht.
|
|
Diese Abbildung zeigt exakt die selbe Struktur wie links, lediglich in einer anderen Ansicht, dem Tetraeder auf eine Kante geschaut. |
|
|
|
|
 |
|
|
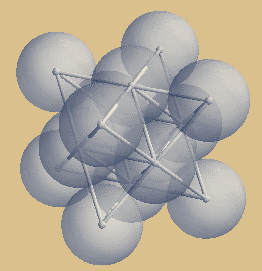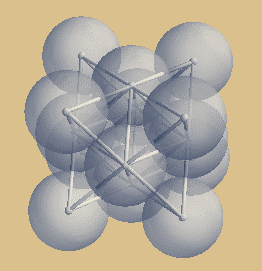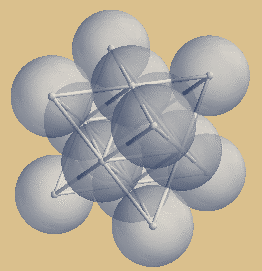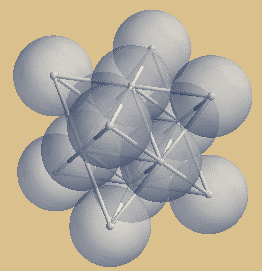
Das Sterntetraeder auch "Keplerstern" oder "Stella Oktangula" genannt, ist genau jener Ausschnitt aus dem kubisch flächenzentrierten Kristallgitter, welcher diese Struktur
ihren Namen verdankt.
Die Mittepunkte der 8 äußeren Kugeln bilden
einen Kubus, diese 8 Kugeln umschließen sechs
innen liegende Kugeln, welche den Oktaederkern
bilden. Jede der 6 Oktaeder-Kugeln trifft genau
das Zentrum der entsprechenden 6 Kubusflächen,
deshalb also kubisch flächenzentriert.
Diese Bezeichnung ist in der Kristallographie
allgemein gültig.
Andere Bezeichnungen sind, wie oben schon
genannt "Kepplersche Kugelpackung" und
"Buckminster Fuller Isotropic Vector Matrix".
Die Konstruktion des Sterntetraeders kann
man auf verschiedene Weise erklären:
1.: Auf den acht Flächen eines Oktaeders sitzt
jeweils ein Tetraeder gleicher Kantenlänge.
2.: Das Sterntetraeder ist der Durchdringungs-
körper von zwei großen Tetraedern, deren
Schnittmenge ein kleines Oktaeder bildet.
3.: Die 12 Kanten eines Kubus von Ecke zu
Ecke bis zum Mittelpunkt der Flächen
rausgeschnitten, ergeben ein Sterntetraeder.
Volumenverhältnisse
Das Volumen-Verhältnis Oktaeder zu
Tetraeder ist 1 zu 4 (Tetraktys!) bei gleicher
Kantenlänge der Körper, also so wie beide
Körper auch im Kristallgitter aneinander
liegen.
|
|
|
|
|
|
|
 |
|
 |
|
 |
|
|
|
|
|
Symmetrie-Ansichten des
Sterntetraeders
|
|
|
| Sterntetraeder mit Kugelpackung |
|
Sterntetraeder mit Kubus-Umriss |
|
Der umspannende Kubus eines Sterntetraeders
hat 8 Tetraeder, 12/4 Oktaeder (rausgeschnittene
Ecken) + 1 ganzes Oktaeder in der Mitte.
Das ergibt zusammen also 4 Oktaeder und 8
Tetraeder.
Der Anteil Oktaeder zu Tetraeder
entspricht 1 : 2.
Somit hat der umspannende Kubus eines
Sterntetraeders das Volumen von 24
Tetraedern oder 6 Oktaedern gleicher
Kantenlänge = 1 zu 4 (Tetraktys).
1 Sterntetraeder hat genau die Hälfte vom Volumen des umspannenden Kubus.
Die Verdoppelung der Kantenlänge entsprechend eines Rekursionsschrittes bzw. einer Iterationsstufe der fraktalen Struktur bewirkt das 8-fache des Volumens aller Körper.
|
|
Oktader-Anteile des Fraktals versechsfachen sich.
Tetraeder-Anteile des Fraktals vervierfachen sich.
Der Kubus als Summe von Tetraeder- und
Oktaeder-Anteilen verachtfacht sich.
Die Struktur enthält doppelt so viele Tetraeder wie Oktaeder, das Oktaeder hat aber das 4-fache Volumen vom Tetraeder.
Somit ist das Volumen-Verhältnis
der gesamten Kristallstruktur zwischen
Oktaeder zu Tetraeder = 2 zu 1.
Hier der Versuch einer Beschreibung, wie
man sich die korrekte geometrische Integration
von raumfüllenden Würfeln innerhalb der lückenlosen Tetraeder-Oktaeder-Struktur vorstellen kann – nicht ganz einfach zu verstehen.
|
|
 |
|
|
|
|
DIE PYTHAGOREISCHE TETRAKTYS – DIE BEDEUTUNG DER 10-ZAHL IM TETRAEDER-FRAKTAL
|
|
 |
|
|
|
|
|
|
 |
|
|
|
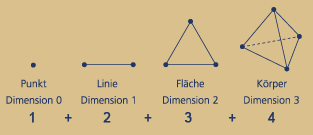
Wie auf der Startseite angemerkt, illustrieren
die drei Dimensionssprünge des Tetraeders:
1 Punkt
1 Linie = Kante = 2 Ecken = 2 Punkte
1 Dreieck = Fläche = 3 Ecken = 3 Punkte
1 Tetraeder = Raum = 4 Ecken = 4 Punkte
|
|
 |
|
|
Wer das Sierpinski-Dreieck bzw. Pascalsche Dreieck kennt, dem ist sicherlich auch bewusst, welche Bedeutung diesem in der Zahlentheorie zukommt.
Insbesondere die hier im Zusammenhang mit der Tetraktys behandelten Simplexe = Tetraeder
in n Dimensionen (!) sind lückenlos im
Pascalschen Dreieck zu finden.
Siehe dazu:
SIMPLEX – MULTIDIMENSIONALE
TETRAEDER, 4. DIMENSION
Das Tetraeder ist ein 3-dimensionales Dreieck. Und das oben bereits dargestellte kubisch
flächenzentrierte Kristallgitter ist korrekt
ein 3-dimensionales Sierpinski-Fraktal!
Solch ein Fraktal kann man sowohl als Tetraeder mit den entsprechenden Oktaederlücken, als auch als Oktaeder mit Tetraederlücken darstellen, so wie rechts zu sehen ist.
Beide Fraktale zusammen genommen, ergeben wieder die lückenlose Raumfüllung so wie oben beschrieben. |
|
|
 |
|
|
|
auf prägnante Weise die Vierheit von
Ecke, Kante, Fläche und 3-D-Raum
nicht aber die Zehnheit einer Pythagoreischen Tetraktys – welcher auch immer.
Denn die Punkte einfach nur zusammen zu zählen hat keine sinngebende Bedeutung.
Halten wir also erst mal fest:
Das Tetraeder ist der einfachste geometrische
Körper, welcher die Dimensionssprünge auch
direkt abbildet siehe Simplexe(!),
aber:
Er ist nicht mit sich selbst im 3-dimensionalen Raum lücklenlos parkettierbar!
Das sollte auch beim Betrachten der Eingangs beschriebenen "lückenlose Raumstruktur" klar geworden sein.
|
|
|
 |
|
|
|
|
|
|
|
 |
|
|
|
 |
|
Was passiert also mit einen Tetraeder, dem Repräsentant unserer dritten Dimension, wenn daraus ein Fraktal wird?
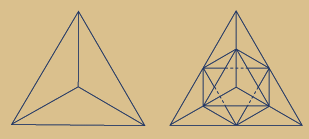
Die kleinste fraktale Einheit, also der erste
Rekursionsschritt (Iterationsstufe) lässt aus
ursprünglich 4 Ecken und 6 Kanten nun
10 Eckpunkte und 24 Kanten entstehen –
ein Tetraeder + Oktaederlücke in der Mitte:
|
|
 |
|
|
|
|
|
Links ein einfaches Tetraeder, rechts das Fraktal
|
|
|
Die 6 Kanten des Tetraeders werden von
den 6 Ecken eines Oktaeders geteilt, womit
dieses zu einem Fraktal mit 10 Ecken wird: |
|
1.
Wenn man bedenkt, dass der Raum mit Tetraeder- und Oktaederzellen unbegrenzt lückenlos parkettierbar ist, dann passiert nach diesem ersten Rekursionsschritt diesbezüglich nichts neues mehr!
2.
Dieses lückenlos Raum füllende "Urfraktal"
mit seinen 10 Ecken (Kugeln!) und 24 Kanten
zeigt die Verbindung zur Tetraktys:
1 + 2 + 3 + 4 = 10 und 1 x 2 x 3 x 4 = 24
Im Zusammenhang mit der Primzahl-
problematik.
3.
Der Anteil Oktaeder zu Tetraeder ist 1 : 2.
Das Volumenverhältnis Tetraeder zu Oktaeder
ist korrekt 1 zu 4. Deshalb befindet sich
das Volumenverhältnis dieser beiden kleinst möglichen Zellen des "Urfraktals"
genau im Gleichgewicht. |
|
 |
|
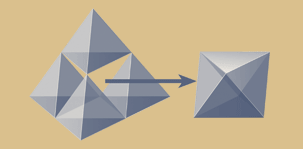
Links ein Tetraeder-Fraktal mit Lücke, rechts das Oktaeder, welches diese Lücke ausfüllt.
Das Bild oben mittig zeigt alle Zellen zusammen als Expolsionsdarstellung, das Bild ganz rechts das "Ur-Fraktal in verschiedenen Ansichten.
Worin liegt also die Bedeutungsschwere?
|
|
|
|
Das "Ur-Fraktal" in verschiedenen Ansichten.
|
|
 |
|
|
|
|
Und zu genau diesem Thema haben sich schon die antiken und spätantiken Denker abgearbeitet: DIE KABBALA – TETRAKTYS MAL ANDERS
|
|
|
 |
|
|
Die Gegenüberstellung von 10-Punkte-Dreieck
und Tetraeder-Fraktal
Im Pascalschen Dreieck finden wir die Dreieckszahlen direkt neben den Tetraederzahlen. Tetraederzahlen ergeben sich aus der Stapelfolge der Kugelschichten eines Tetraeders, diese entsprechen wieder den Dreieckszahlen.
Unser "Urfraktal" hat die Stapelfolge von
1, 3 und 6 – also insgesamt 10 Kugeln:
|
|
 |
|
|
|
|
Die aufkumulierte Menge vor dem 10-Punktedreieck ist 10. 10 = 10
|
|
|
|
 |
|
|
 |
|
Wenn man sich nun wieder dem 10-Punkte-
Dreieck zuwendet, dann stellt man fest, dass
die Ziffern 6 und 10 und die entsprechende
Differenz von 4 uns etwas sagen wollen.
Dass diesen ein Ordnungsprinzip zu Grunde liegt, welches auch in der Zahlentheorie zu finden ist.
|
|
Innerhalb des 6-Punkte-Dreiecks haben wir ebenfalls einen "Punke-Gleichstand". Zu drei Punkten
kommen drei Punkte hinzu.
Details unter: DAS PUNKTEDREIECK, EINFACH NUR 1 + 2 + 3 + 4 = 10 ?
|
|
 |
|
|
DIE TETRAKTYS VON TETRAEDER, OKTAEDER, KUBOOKTAEDER UND STERNTETRAEDER
|
|
 |
|
|
|
Wenn man sich nun weiter in diese äußerst
interessante Geometrie reindenkt und die
Entsprechung zur Zahlentheorie herstellt, dann
erkennt man schnell, dass hier der Weg noch
nicht zu Ende ist!
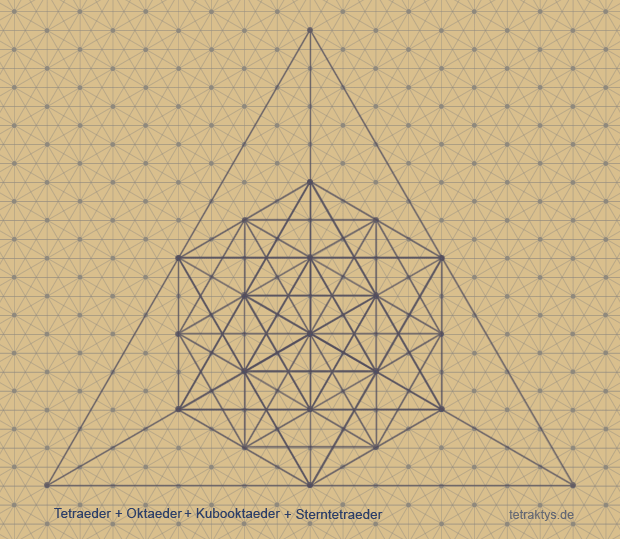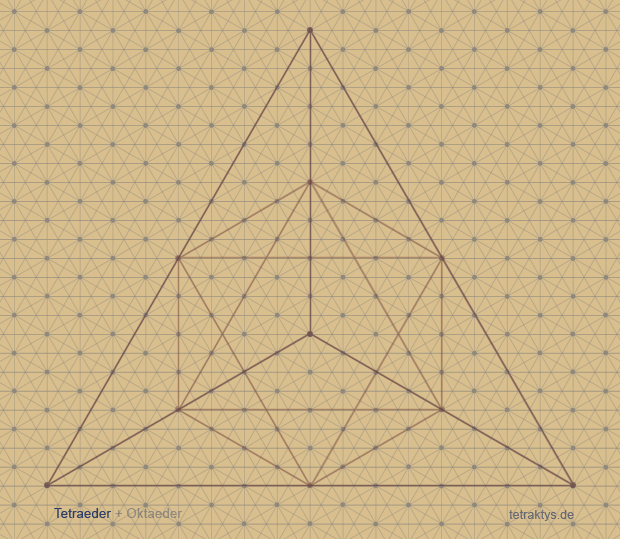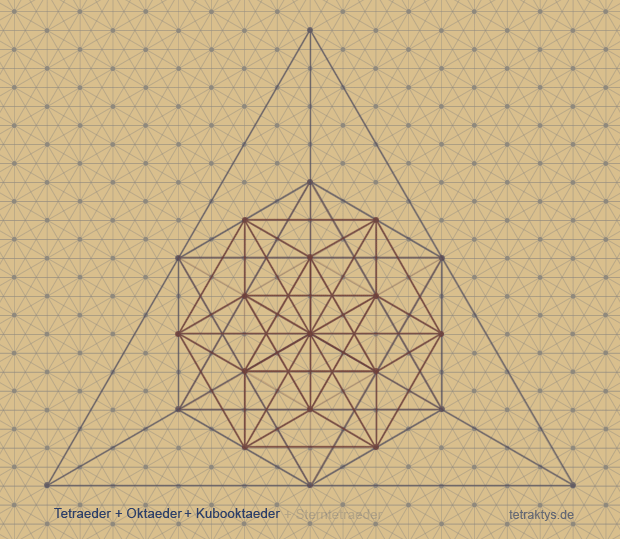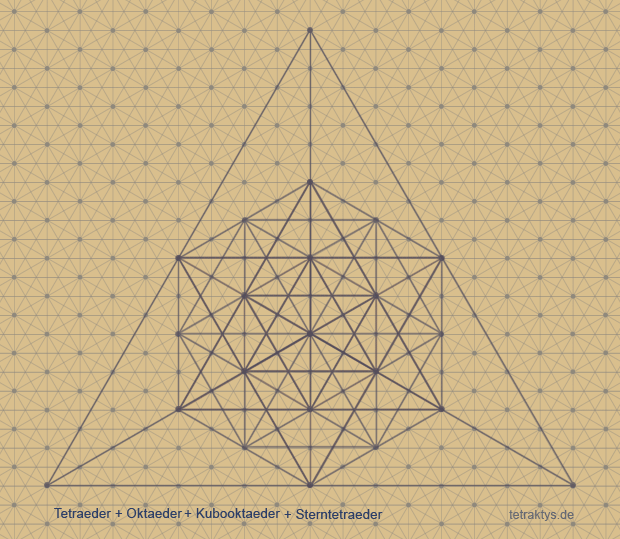
Denn mit zunehmender Verdichtung des Fraktals bildet die Tetraeder-Oktaeder-Struktur zwei weitere wichtige Symmetrien,
also insgesamt vier = Tetraktys (!),
In folgenden Rekursionsschritten aufkumuliert:
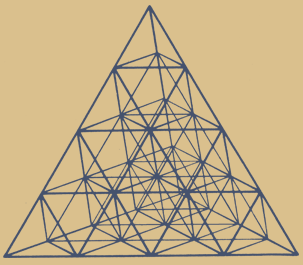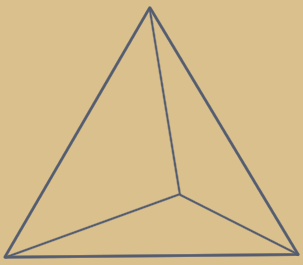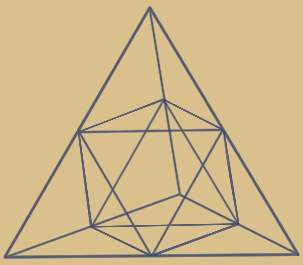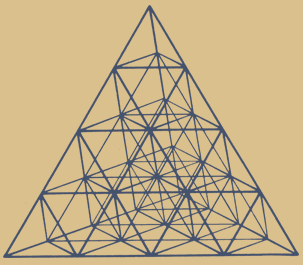
0. Tetraeder
1. Tetraeder + Oktaeder
2. Tetraeder + Oktaeder + Kubooktaeder
3. Tetraeder + Oktaeder + Kubooktaeder
+ Sterntetraeder, (Kubus-Umriss)
Was macht diese beiden neu hinzu kommenden Körper so interessant? Sterntetraeder und Kubooktaeder weisen verschiedene Dualitäten und Durchdringungen zu zwei weiteren interessanten Symmetrien auf:
Das Rombendodekaeder und der Hexaeder (Kubus)!
Diese Körper können sich zwar nicht direkt
aus Oktaeder- und Tetraeder-Zellen zusammensetzen. Durch neue Verbindungen der Eckpunkte (Kugelmittelpunkte) spannt sich jedoch eine neue Gitterstruktur auf. Und:
Rombendodekaeder und Hexaeder sind nun auch mit sich selbst im Raum parkettierbar!
Sterntetraeder und Kubooktaeder sind also sozusagen die "Partner und Vermittler" dieser neuen Gitterstruktur im alten Tetraeder-Oktaeder-Netz und bilden die bestmögliche Symmetrie innerhalb dieser Struktur.
|
|
 |
|
 |
|
|
DIE RAUMWINKELSUMME EINER VOLLEN KUGEL UND DIE DARAUS RESULTIERENDE SYMMETRIE
|
|
 |
|
|
|
In KREIS, DREIECK & QUADRAT
ist darauf eingegangen worden, dass es nur drei
regelmäßige Vielecke bzw. Polygone gibt,
die mit sich selbst lückenlos parkettierbar sind:
Dreieck, Quadrat und Sechseck, wobei sich das Sechseck lediglich aus Dreiecken zusammensetzt.
Es handelt sich dabei um die so genannten
platonischen Parkettierungen.
Das wiederum hat damit zu tun, dass alle Winkel
um jeden Eckpunkt innerhalb einer Parkettierung
zwingend einen vollen Kreis, also 360 Grad
ergeben müssen.
(4-Ecke 4x 90Grad, 3-Ecke 6x 60 Grad,
6-Ecke 3x 120 Grad)
Zwingenderweise sind auch die Eckpunkte
des dreidimensionalen Raumes nur mit
Raumwinkelsummen zu füllen, die
eine volle Sphäre (Kugel) ergeben.
Die Körper, welche diese Bedingung erfüllen können, sind wieder nur aus 3- und 4-Eck-Flächen zusammengesetzt und dürfen auch nur 3-, 4-
und 6er Symmetrien aufweisen.
Um solch einen Kugelmittelpunkt spannen sich zwei zueinander komplementäre Symmetrien,
|
|
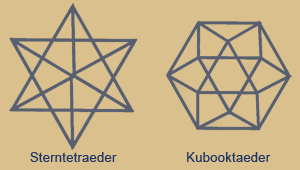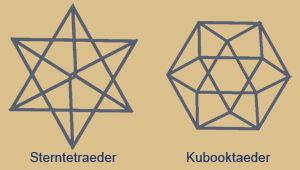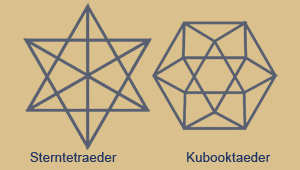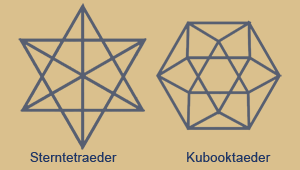
das konkave Sterntetraeder und das
konvexe Kubooktaeder.
Beim Kubooktaeder weisen die Tetraeder- und
Oktaeder-Ecken nach innen und entsprechen
dem Mittelpunkt einer Kugel!
|
|
Beim Sterntetraeder dagegen weisen all diese Ecken nach außen, das Sterntetraeder hat
keinen Kugelmittelpunkt, solange es kein Fraktal bildet.
(Die 2D-Animation kann das leider nicht zeigen,
sehr gut zu sehen ist das dagegen am Modell
direkt darunter stehendes Foto Mitte!)
Auf Grund Ihrer Beziehung innerhalb der
fraktalen Struktur sind beide Körper
dennoch ineinander verschachtelt!
Beiden Körpern ist – bedingt durch die Kombinatorik von 3, 4 und 6
eine 12er und 24er Symmetrie eigen.
Die kleinsten Zellen dieser Körper bleiben
jedoch Tetraeder und Oktaeder!
Jeder Knotenpunkt (Kugel) der fraktalen Struktur
setzt sich immer aus 6 Oktaederecken und 8 Tetraederecken zusammen, dies entspricht einem Kubooktaeder.
Genau die selbe Eckenkonstellation ist bei
einem Sterntetaeder nach außen gerichtet,
die Raumwinkelsumme dieser Ecken
entspricht demnach einer vollen Kugel.
|
|
 |
|
|
 |
|
 |
 |
|
|
Das Ur-Fraktal, die erste mögliche Oktaeder-Tetraeder-Verbindung: 10 Eckpunkte bzw. Kugeln und 24 Verbindungen bzw. Kanten.
|
|
Konkave Symmetrie des Sterntetraeders. Die Ecken der Oktaeder- und Tetraeder-Zellen weisen nach außen! |
|
Konvexe Symmetrie des Kubooktaeders, Die Ecken der Oktaeder- und Tetraeder-Zellen weisen nach innen auf den Kugel-Mittelpunkt! |
|
 |
|
|
|
|
|
|
|
 |
|
|
|
|
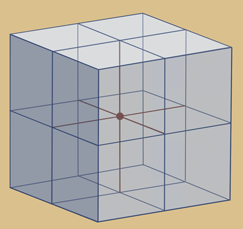
Auch die Raumwinkelsumme eines Kubus bzw. Hexaeders hat eine volle Kugel.
Auf einen Kugelmittelpunkt übertragen heißt
dies, dass sich 8 x-y-z-Achsen, also 8-Achtel
Kugeln zur Raumwinkelsumme einer
vollen Kugel vereinigen:
|
Da die Winkelsummen in Einheiten voller
Kreise auch bei zweidimensionalen
Polygonen und Sternpolygonen in
auffälliger Weise mit zahlentheoretischen
Entsprechungen korellieren, ist mit Recht
davon auszugehen, das dies auch für
den 3D-Raum gilt.
Dieser Verdacht verstärkt sich in Anbetracht
der Tatsache, das Symmetrien um einen Kugelmittelpunkt sehr oft 24-zählig sind.
Siehe dazu auch:
KUSSZAHLEN, KUGELPACKUNGEN
UND DIE ZAHL 24
oder ausführlicher:
BEMERKENSWERTES ZUR ZAHL 24 ( 25 - 1 )
|
|
|
 |
|
|
Die Entsprechung in der zweiten Dimension:
Das Viereck ist das einzige Polygon mit der Winkelsumme eines vollen Kreises, das Hexagramm (2-dimensionales Sterntetraeder) ist das einzige aus Polygonen zusammengesetzte Sternpolygon mit der Winkelsumme eines vollen Kreises.
|
|
 |
|
|
|
|
|
|
|
Nebenstehende Animation zeigt
die vier Symmetrien des Kristallgitters der kubisch flächenzentrierten Kugelpackung: Tetraeder,
Oktaeder,
Kubooktaeder,
Sterntetraeder (Kubus-Umriss)
Das Sterntetraeder zeigt die Durchdringung zweier Tetraeder,
dessen Schnittmenge ein Oktaeder bildet. Das Kubooktaeder zeigt die Schnittmenge von Kubus und Oktaeder.
Sterntetraeder und Kubooktaeder haben selbst ebenfalls eine komplementäre Beziehung wie oben beschrieben.
Das Rombendodekaeder und
der Kubus bilden eine eigene
Gitterstruktur:
das Kristallgitter der kubisch innenzentrierten Kugelpackung
Jedoch: Der Kubus ist dual zum Oktaeder, das Rombendodekader
ist dual zum Kubooktaeder.
|
|
|
Seit einiger Zeit gibt es im Internet viele Beiträge
und Videos von einem jungen hemdsärmeligen
italienischen Hobbyphysiker namens
Nassim Haramein, der diese Matrix zur
Weltformel erklärt hat.
Meiner Meinung nach nicht ganz zu Unrecht.
Über die fachliche Kompetenz seiner Theorien
kann ich mir natürlich kein Urteil bilden.
Seine Darstellung und Interpreation dieser
Geometrie aber ist durchaus recht anschaulich, lehrreich und vor allem sehr unterhaltsam.
Hier ein Video mit deutschen Untertiteln:
http://vimeo.com/6721901
|
|
 |
|
|
 |
|
|
|
Hier noch mal der Link zur PDF
von verschiedenen Modellansichten als Kugelpackung und Kristallgitter:
Modellansichten – kubisch flächenzentriertes Kristallgitter
|
|
|
Dieses Thema wird noch bearbeitet. Bitte schauen Sie zu einen späteren Zeitpunkt wieder vorbei.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|