|
|
|
|
|
|
|
|
|
|
|
| INHALT: |
|
 |
|
|
|
Der Naturwissenschaftler
In allen Bereichen des Quadriviums – des mathematischen Teils der "sieben freien Künste" – werden ihm wesentliche Erkenntnisse zugeschrieben. Es handelt sich um Arithmetik, Geometrie, Astronomie und Musik. |
|
Hinzu kommt die Heilkunst, die man gewisser-
maßen als die Umsetzung der Erkenntnisse aus
Philosophie und Naturwissenschaft in die Praxis bezeichnen kann.
Pythagoras erscheint uns geradezu als Naturwissenschaftler im modernen Sinn, wenn wir erfahren, dass er das "Vorausdenken durch Zahlen" höher einschätzte als die Opferschau.
Die Begründung, die wir hierfür bei Imablichos finden, zeigt und darüber hinaus den Denker nach dem Analogieprinzip, das uns westlichen Menschen seit Descartes weitgehend abhanden gekommen ist.
Pythagoras hielt nämlich das Vorrausdenken durch Zahlen "den himmlischen Zahlenverhältnissen der Götter entsprechend".
Der Begriff der Analogie führt uns zu dem bedeutungsreichen griechischen Wort "logos", das auch mit der "Proportion" übersetzt werden kann.
Der Vergleich mehrerer "logoi" wurde schon in der Antike mit "Analogia" bezeichnet.
So hatte Pythagoras vor zweieinhalb Jahrtausenden die Anregung geliefert für die schon erwähnte harmonikale Grundforschung, die an einem Institut der Hochschule für Musik in Wien mit beachtlichen Ergebnissen proportionale Entsprechungen in den Strukturen der Schöpfung aufgespürt hat, welche überwiegend als wohlklingende Intervalle darstellbar sind.
Der Arithmetiker
Für den Arithmetiker Pyhagoras waren Zahlen
keine abstrakten Größen, sondern konkrete Bezugspunkte "in einer als Logos verstandenen Reihenbildung – etwa in den Tonleitern – ,
|
|
die durch das Medium der Musik nicht nur materiell-quantitativ, sondern auch seelisch-geistige Werte (Qualitäten) mittels Gehörsinnes empfunden bzw. erlebt werden können".
Es wird hier deutlich, wie schwer es ist, bei Pythagoras die einzelnen Wissenschaftszweige voneinander zu trennen.
Der analoge Denker blickt bei allen Erkenntnissen über den Zaun und sucht nach Entsprechungen; eine Methode, die in unseren heutigen Universitäten durchaus noch förderungswürdig ist.
Das Analogieprinzip wird auch bei der so genannten Tetraktys deutlich, jener Vierheit, die sich in den ersten vier Zahlen manifestiert. Ihre Summe ergibt die heilige Zahl Zehn.
Wir ließen Walter Kranz bei der Behandlung der philosophischen Lehre des Pythagoras dazu bereits zu Wort kommen.
Dennoch sei das Wesentliche hier mit dem Blick auf den Arithmetiker und analogen Denker wiederholt.
Die Tetraktys ist eine Zahlenoperation, die in der Musik ihren Ursprung hat: Bei seinem Versuch auf dem Monochord – einem mit einer Saite bespannten Resonanzkörper – entdeckte Pytagoras, dass sich bei den wohlklingenden Intervallen – der Oktave, der Quinte und der Quarte – die Saitenlängen zueinander wie 1:2, 2:3, und 3:4 verhielten. Es ergab sich also dreimal das Verhältnis einer ungeraden Zahl zu einer geraden Zahl.
Man beachte die mathematisch-philosophische Querverbindung: Die Gesetzmäßigkeiten der Tetraktys wurden auf die in der Welt herrschenden Gegensätze übertragen. Die Vier als die erste Quadratzahl wurde zur heiligen Zahl.
|
|
 |
|
 |
|
|
|
Der Geometer
Wenden wir uns der Geometrie zu, so denken wir, natürlich zuerst an den berühmten "Pythagoreischen Lehrsatz", der besagt: In einem rechtwinkligen Dreieck ist der Flächeninhalt des Quadrates über der Hypotenuse gleich der Summe der Flächeninhalte der Quadrate über den Katheten. Auf diesen Lehrsatz beruht z.B. die Definition des Abstandes zweier Punkte in der analytischen Geometrie.
Ob der pythagoreische Lehrsatz auf Pythagoras selbst zurückgeht ist nicht nachweisbar.
Platon jedenfalls kannte ihn (gute hundert Jahre später), wie aus seinem "Menon" hervorgeht.
Bekannt, wenn auch nicht bewiesen, war der Satz schon den alten Babyloniern. Die pythagoreischen Zahlentripel, d.h. jeweils drei natürliche Zahlen, zwischen denen die Beziehung des Pythagoreischen Lehrsatzes besteht (z.B. 3:4:5), finden sich bereits auf babylonischen Tabellen, die auf das 3. Jahrtausend vor Christus zurückgehen.
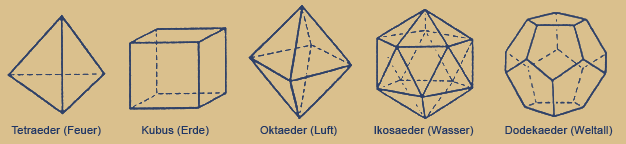
Die Entdeckung des Pentagon-Dodekaeders jedoch dürfte mit Sicherheit den Pythagoreern zuzuschreiben sein.
Dieser von zwölf kongruenten Fünfecken begrenzte geometrische Körper erregte seinerzeit höchste Aufmerksamkeit, da er die bis dahin gültige Ordnung der Weltzahl Vier durchbrach.
Die bisher bekannten vier regelmäßigen Körper,
die dadurch gekennzeichnet sind, dass man
ihnen je eine Kugel ein- und umbeschreiben kann,
waren der Tetraeder (aus vier gleichseitigen
Dreiecken, d. i. eine Pyramide mit dreieckiger
Grundfläche), der Kubus (Hexaeder; aus sechs
Quadraten), der Oktaeder (aus acht
gleichseitigen Dreiecken, also zwei aufeinander
gesetzte Pyramiden mit quadratischer
Grundfläche) und der Ikosaeder (aus zwanzig
gleichseitigen Dreiecken).
|
|
|
Die geometrische Erfahrung, dass man nur mit gleichseitigen Dreiecken oder Vierecken den Raum um einen gegebenen Punkt herum gleichmäßig begrenzen kann, hatte grundsätzliche Konsequenzen für das Weltbild jener Zeit.
Wir können dieses Denken deshalb gut nachvollziehen, weil uns Platon in seinem Dialog zwischen Sokrates und dem pythagoreischen Philosophen Timaios die Zusammensetzung der Welt aus lauter unendlich kleinen Dreiecken beweist.
Die kleinste Fläche kann nur ein Dreieck sein, da dieses die geringstmögliche Seitenzahl hat und durch Teilung immer wieder ein Dreieck ergibt.
Der kleinste Körper kann also nur aus Dreiecken gebildet werden, und zwar aus gleichseitigen, weil diese die "schönsten" sind.
"Warum das so ist", sagt Platon, "wäre eine zu weitläufige Untersuchung"; aber er verspricht demjenigen, der diese Behauptung widerlegt, den Siegerpreis des Dialogs. Da die ideale und schönste Form die Kugel – die "Sphäre" – ist, muss der Körper in eine Kugel einzupassen und
um diese herum zu konstruieren sein.
Für den Kubus wird ausdrücklich betont, dass
seine quadratischen Seitenflächen ja aus vier gleichschenkligen Dreiecken "von der Natur zusammengesetzt wurden, indem die rechten Winkel im Zentrum zusammenstießen", so dass die göttliche und schöpferische Zahl Drei – Die heilige Zahl – auch im rechtwinkligen Viereck waltet.
|
|
Die vier bekannten Körper wurden nun logischerweise den vier Grundbestandteilen der Schöpfun, den Elementen Feuer, Erde, Wasser, Luft zugeordnet.
Hierbei fiel der Kubus auf des Element Erde, "denn unter den vier Gattungen ist Erde am unbeweglichsten und unter den Körpern am bildsamsten, für sie ist es am meisten nötig, dass sie die sichersten Grundflächen hat." Damit wurde eine uralte Tradition neu begründet: Drei war die Zahl der Götter, vier die der Erde.
In diese festgefügte Ordnung platzte nun die Entdeckung des Pentagon-Dodekadeders wie eine Bombe ein. Bisher unumstürzliche Denkkategorien wurden umgeworfen. Dies musste an die Grundfesten des Weltverständnisses der damaligen Zeit rühren.
Ein Körper, der nicht aus Dreiecken zu konstruieren war, sollte die gleichen Eigenschaften vorweisen können, wie die bisher bekannten; nämlich in die "Sphäre" (Kugel) einzupassen sein?
Diese Entdeckung wurde wahrscheinlich aus Klugheit und Vorsicht von den Pythagoreern als strenges Geheimnis gehütet.
Von dem Entdecker jenes "unmöglichen" Körpers berichtet denn auch Iamblichos: "da er aber erstmals schriftlich das Geheimnis der einem Pentagon-Dodekaeder umbeschriebenen Kugel an die Öffentlichkeit gebracht habe, sei er als Mysterienverräter im Meer umgekommen".
Platon machte aus dieser Not eine Tugend und ordnete den neuen Körper als den fünften dem Weltall zu.
|
|
 |
|
 |
|
|
|
Der Astronom
Pythagoras soll als erster die Kugelgestalt der
Erde angenommen haben. So jedenfalls berichtet uns der vorsokratische Philosoph Parmenides
(ca. 540-470).
Um seinen "Globus", der im Mittelpunkt des
Kosmos ruht, kreisen nach jener Theorie die
ebenfalls kugelförmigen sieben Himmelskörper,
die damals bekannten fünf Planeten sowie Sonne
und Mond. Desgleichen dreht sich der ganze Fixsternhimmel um die Erde.
Dies war der Anfang grandioser astronomischer
Fortschritte; denn bald darauf hören wir von der
pythagoreischen Lehre, dass die Erde sich in
konzentrischen Kreisen zugleich mit den sieben
Sphären und mit einem ihr entsprechenden, nur
hypothetisch erschlossenen Gegenbild, der sogenannten Gegenerde, um ein Zentralfeuer herum" bewegen, dem sogenannten "Herd des Alls".
Hier wird also die Erde bereits nicht mehr als Mittelpunkt des Alls angesehen.
Welch ein Schritt in die richtige Richtung, wenn
wir bedenken, dass danach seit Platon wieder
|
|
das geozentrische Weltbild festgeschrieben
wurde und als sogenanntes ptolemäisches
Weltbild bis über Kopernikus (1473–1543), den
Begründer des heliozentrischen Weltbildes,
hinaus geradezu zur Glaubensprüfung wurde,
wie Galileo Galilei (1564_1642) erfahren
musste.
Um die Wende vom 5. zum 4. Jahrhundert lehrten die Pythagoreer Hiketas und Ekphantos sogar
die Drehung der Erde um ihre Achse vom
Westen nach Osten.
|
|
 |
|
|
 |
|
|
 |
|
|
Der Musiktheoretiker
Pythagoras war, wie wir bereits feststellten, ein Pionier in der Erforschung musikalischer Gesetze. Iamblichos beschreibt in allen Einzelheiten seine akustischen Versuche, die allerdings einer genauen Nachprüfung nicht standhalten.
Vielleicht liegt das aber nur daran, dass Iamblichos selbst zu wenig Fachmann war, um jene Versuch korrekt wiederzugeben. Immerhin ist die Legende gefällig, mit der er die Eingebung des Pythagoras zu seiner akustischen Forschung erklärt.
Danach "ging er an einer Schmiede vorbei und hörte – Gute Geister fügten es gerade so – wie die Hämmer das Eisen auf dem Amboss schlugen und im Wechsel die Klänge einander in harmonischen Intervallen antworten ließen (nur ein einziges Paar ausgenommen).
|
|
Er erkannte darin Oktav, Quint, und Quart". Iamblichos berichtet nun nach weiteren Einzelheiten zu den Klangqualitäten, wie Pythagoras in die Schmiede eilte und durch Versuche herausfand, dass der Unterschied in der Tonhöhe von der Masse des Hammers abhängt und nicht von der Gewalt des Hämmernden, von der Gestalt des Hammers oder der Lage des geschlagenen Eisens."
Darauf hin soll er das Gewicht der Hämmer ermittelt haben und nach Hause geeilt sein, um sofort mit seinen Versuchen an Saiten zu beginnen.
Iamblichos schließt diesen Bericht mit der Feststellung: "So soll er die Musik erfunden haben. Und nachdem er sie in ein System gebracht hatte, gab er sie seinen Schülern weiter als Helferin zu allem Edlen."
Wenn wir auch Iamblichos nicht folgen wollen, Pythagoras als Erfinder der Musik zu bezeichnen, so geht doch die Entdeckung, dass sich musikalische Intervalle durch Zahlenverhältnisse darstellen lassen, sicherlich auf die Pythagoreer zurück.
Die Tragweite dieser Entdeckung kann ermessen werden, wenn man weiß, dass bei der Fortsetzung des schon beschriebenen Experiments am Monochord in gleicher Art eine Intervallreihe erklingt, die identisch ist mit der so genannten Natur-Obertonreihe.
Entdeckt wurden diese bei jeder natürlichen Tonerzeugung mitschwingenden Obertöne erst im 17. Jahrhundert, also über zweitausend Jahre später.
Der Musikwissenschaftler Friedrich Zipp stellt hierzu fest: Die Pythagoreer fanden "mittels eines rational-mathematischen Verfahrens – ohne es zu wissen – ein akustisches Naturgesetz.
Dies bedeutet die Sichtbarmachung eines sowohl in der Natur als auch im Menschen selber verankerten Ordnungsprinzips."
Dass die jenen Intervallen zugrunde liegenden Proportionen in der Natur und im Kosmos durchaus in der Überzahl sind, hat die harmonikale Grundforschung an zahlreichen Beispielen nachgewiesen.
|
|
Dass wir Menschen sie als konsonant empfinden, ist in unserer Psyche angelegt. So sind wir "harmonisch" eingebettet in das kosmische Prinzip. Diese Erkenntnis hat Pythagoras bereits aus ältestem Mysterienwissen übernommen.
Er hat darin das Geheimnis der Tetraktys eingebracht, das Operieren mit der Vierheit, und wir denken an den altpyhtagoreischen Sinnspruch:
"Was ist das Orakel von Delphi? Die Tetraktys. Das ist auch die Harmonie der Sirenen".
Diese dunklen Worte weisen uns hin auf das Wissen der ewigen Gesetzmäßigkeiten. So, wie "Delphi" wörtlich "Mutterschoß" bedeutet – hier der Mutterschoß der Erde, aus dem alles Leben hervorgeht, – so enthält das Wesen der Zahl alle Gesetzmäßigkeiten von Himmel und Erde.
Die Musik bringt diese zum Klingen und lässt unsere Seele mitschwingen in göttlicher Harmonie; ist sie doch selbst, wie jene, göttlichen Ursprungs. In den Sirenen verkörpert sich die Musik in ihrer ganzen dämonischen Kraft, der kein Mensch widerstehen kann.
Aus dieser Sicht ist die Übertragung der musikalischen Gesetzmäßigkeiten auf das All, ist der Glaube an die Musik der Sphären geradezu eine Notwendigkeit.
Der jüngere Zeitgenosse von Pythagoras, der Naturphilosoph Heraklit von Ephesus (536–470 v.Chr.), hat diese Gedanken einer Urharmonie philosophisch erweitert und sieht darin die verborgene Übereinstimmung im Wechselspiel entgegen gerichteter Kräfte.
"Harmonia aphanes – verborgene Harmonie" nennt er das, was wir heute als Polaritätsgesetz bezeichnen, jene Urspannung, aus der allein Neues hervorgeht, jene Gegensätze, die in Wirklichkeit Teile einer Ganzheit sind: " Denn es gäbe keine Harmonie, wenn es nicht hoch und tief gäbe, und keine Lebewesen, wenn nicht die Gegensätze weiblich – männlich wären."
Eine ganze Philosophie des Friedens ließe sich
an diese Worte Heraklits anschließen.
|
|
 |
|
|
|
 |
|
|
|
|
|
|
|
| INHALT: |
|
|
|
^ Zurück nach oben ^
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|